Information Field Theory
Information field theory (IFT) is information theory, logic under uncertainty, applied to fields. A field can be any quantity defined over some space, such as the air temperature over Europe, the magnetic field strength in the Milky Way, or the matter density in the Universe. IFT describes how data and knowledge can be used to infer field properties. Mathematically it is a statistical field theory and exploits many of the tools developed for such. Practically, it is a framework for signal processing and image reconstruction. IFT is fully Bayesian. How else can infinitely many field degrees of freedom be constrained by finite data? It can be used without the knowledge of Feynman diagrams. There is a full toolbox of methods. It reproduces many known well working algorithms. This should be reassuring. And, there were certainly previous works in a similar spirit, like Bayesian Field Theory (BFT). See below for IFT & BFT publications and previous works. Anyhow, in many cases IFT provides novel rigorous ways to extract information from data.
Highlights
Radiation biology, radio astronomy and cosmic rays using information field theory
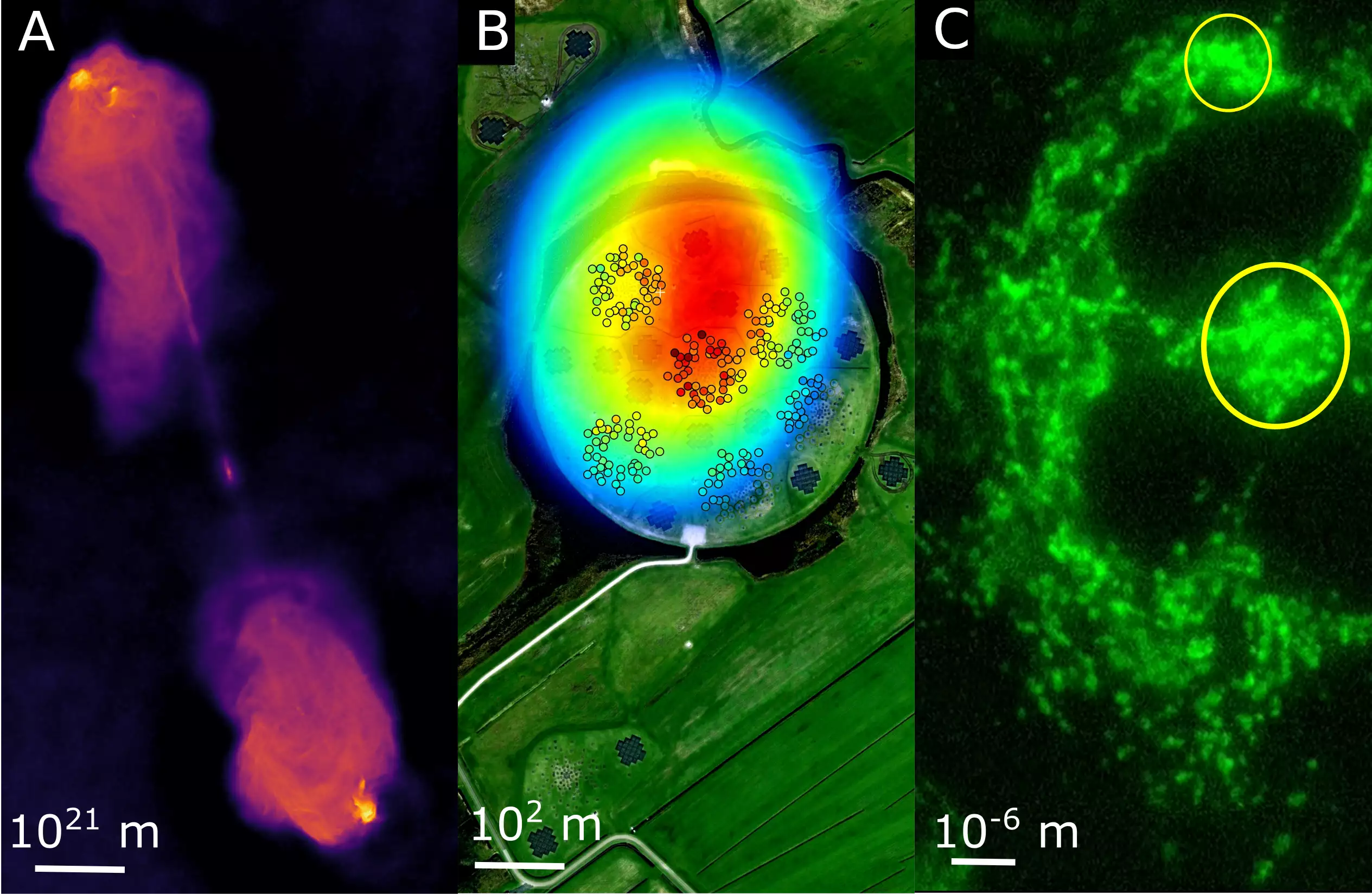
What do radiation biology, radio astronomy and cosmic ray measurements have in common? For one thing, radiation occurs in all of them. For another, all of these fields are explored using large-scale research facilities and require intelligent algorithms to visualize the quantities that occur in the process. In order to advance this imaging in an interdisciplinary way, the Federal Ministry of Education and Research (BMBF) is now funding the project "Information Field Theory for Experiments at Large-scale Research Facilities". Seven German universities, the Max Planck Institute for Astrophysics (MPA) and Erium GmbH, founded by former MPA students, are involved.
- Learn more
Black hole as video: M87* in time, space and frequency

In April 2017 the Event Horizon Telescope (EHT) observed the super-massive black hole M87* and provided a first image of its shadow that went around the world. Researchers at the Max Planck Institute for Astrophysics have now reconstructed a video of the immediate surroundings of a black hole from the same underlying data. This not only confirms previous findings, video of the immediate surroundings of a black hole from the same underlying data. This not only confirms previous findings, it also hints at new structures and dynamics in the gas disk around the black hole.
Watch stars move around the Milky Way’s supermassive black hole in deepest images yet
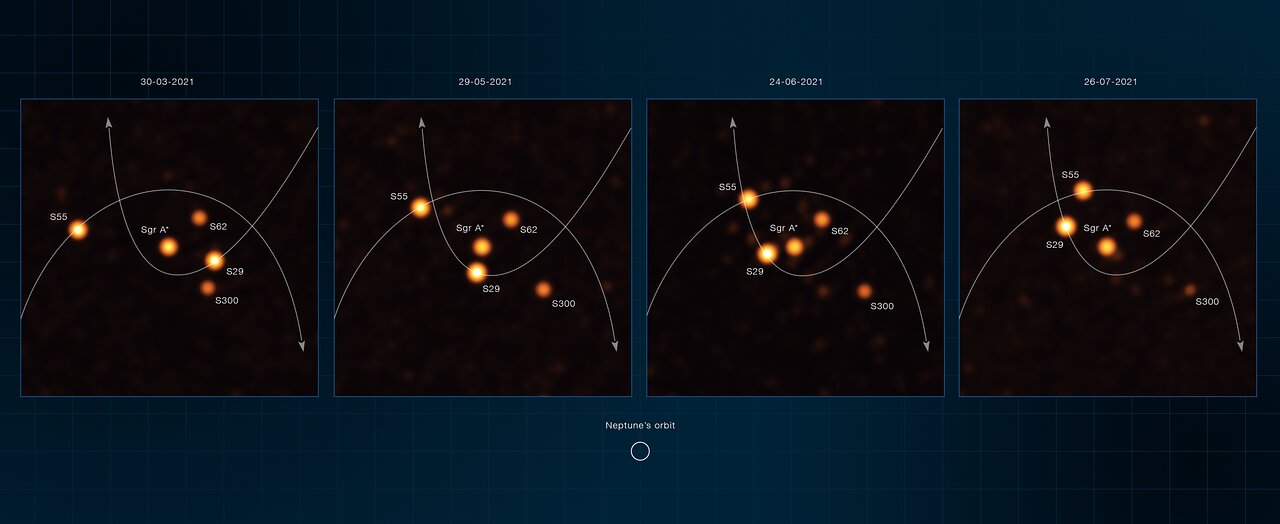
The European Southern Observatory’s Very Large Telescope Interferometer (ESO’s VLTI) has obtained the deepest and sharpest images to date of the region around the supermassive black hole at the centre of our galaxy. The new images zoom in 20 times more than what was possible before the VLTI and have helped astronomers find a never-before-seen star close to the black hole. By tracking the orbits of stars at the centre of our Milky Way, the team has made the most precise measurement yet of the black hole’s mass.
Algorithmic improvements for radio interferometry

Radio telescopes observe the sky in a very indirect fashion. Sky images in the radio frequency range therefore have to be computed using sophisticated algorithms. Scientists at the MPI for Astrophysics have developed a series of improvements for these algorithms, which help to improve the telescopes' resolution considerably.
Artificial intelligence combined

Artificial intelligence expands into all areas of the daily life, including research. Neural networks learn to solve complex tasks by training them on the basis of enormous amounts of examples. Researchers at the Max Planck Institute for Astrophysics in Garching have now succeeded in combining several networks, each one specializing in a different task, to jointly solve tasks using Bayesian logic in areas none was originally trained on. This enables the recycling of expensively trained networks and is an important step towards universally deductive artificial intelligence.
Next generation imaging

The Information Field Theory Group at the Max Planck Institute for Astrophysics has released a new version of the NIFTy software for scientific imaging. NIFTy5 generates an optimal imaging algorithm from the complex probability model of a measured signal. Such algorithms have already proven themselves in a number of astronomical applications and can now be used in other areas as well.
The embarrassment of false predictions -
How to best communicate probabilities?
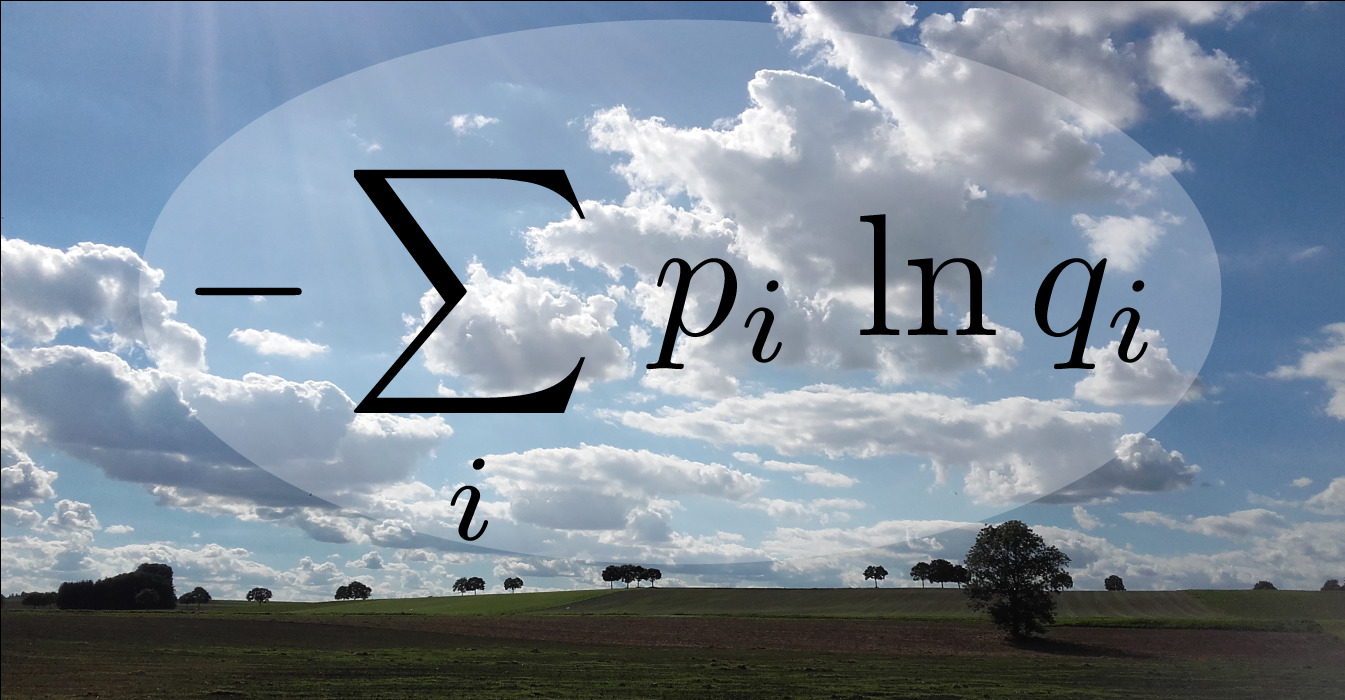
Complex predictions such as election forecasts or the weather reports often have to be simplified before communication. But how should one best simplify these predictions without facing embarrassment? In astronomical data analysis, researchers are also confronted with the problem of simplifying probabilities. Two researchers at the Max Planck Institute for Astrophysics now show that there is only one mathematically correct way to measure how embarrassing a simplified prediction can be. According to this, the recipient of a prediction should be deprived of the smallest possible amount of information.
Galactic anatomy with gamma rays
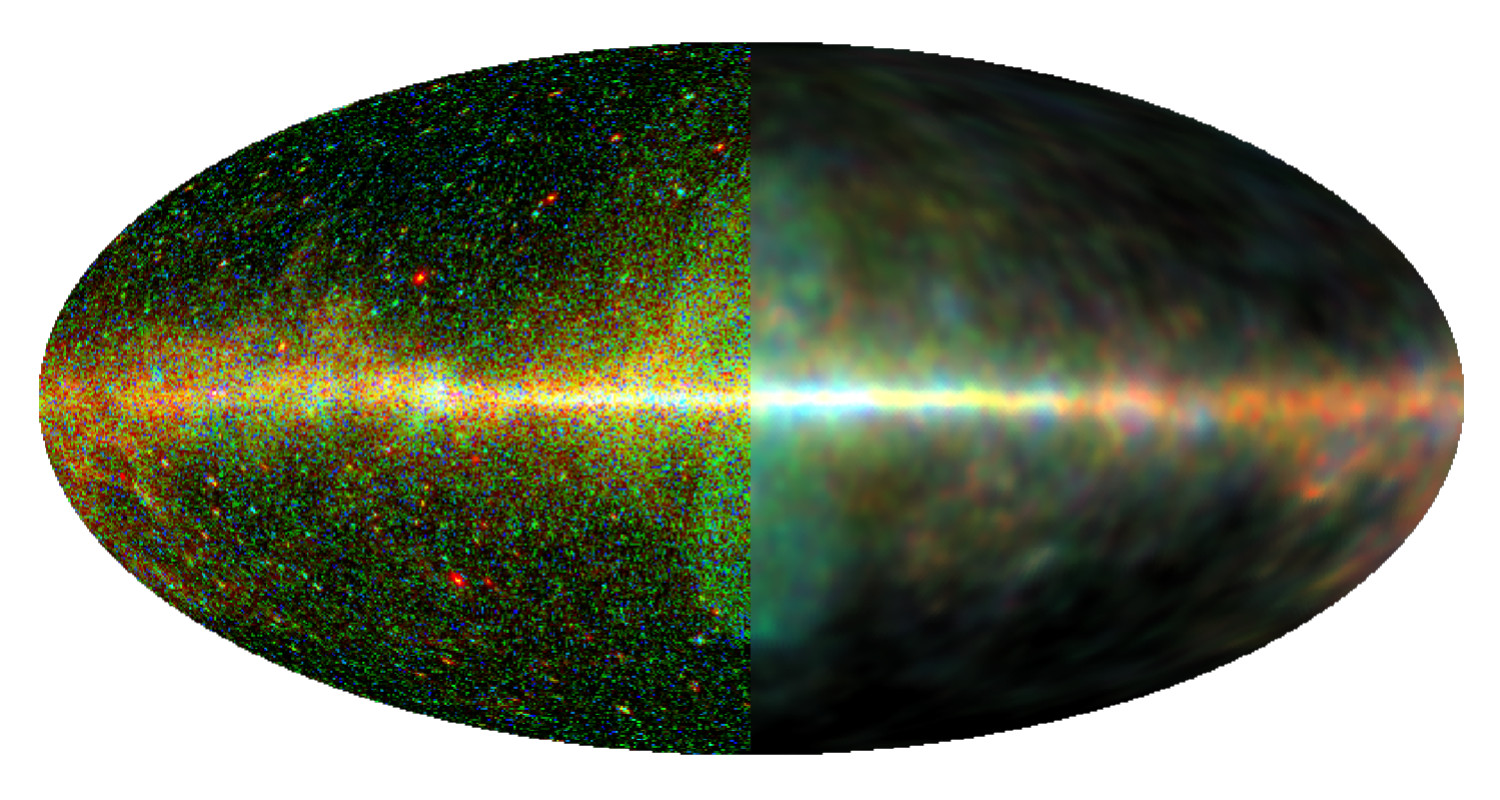
The anatomy of the Milky Way as seen in gamma light is full of mysteries. For example, there are gigantic bubbles of unknown origin above and below the center of the Milky Way that emit a lot of this high-energy radiation. A new method for imaging, developed at the Max Planck Institute for Astrophysics, now divided the Galactic gamma-radiation into three fundamental components: radiation from point sources, radiation from reactions of energetic protons with dense cold gas clouds, and radiation from electrons scattering light in the thin, hot, Galactic gas. The anatomic insights gained unravel some Galactic mysteries. Thus, it appears that the gamma-ray bubbles are simply outflows of ordinary, hot gas from the central region of the Milky Way.
New all-sky map shows the magnetic fields of the Milky Way with the highest precision
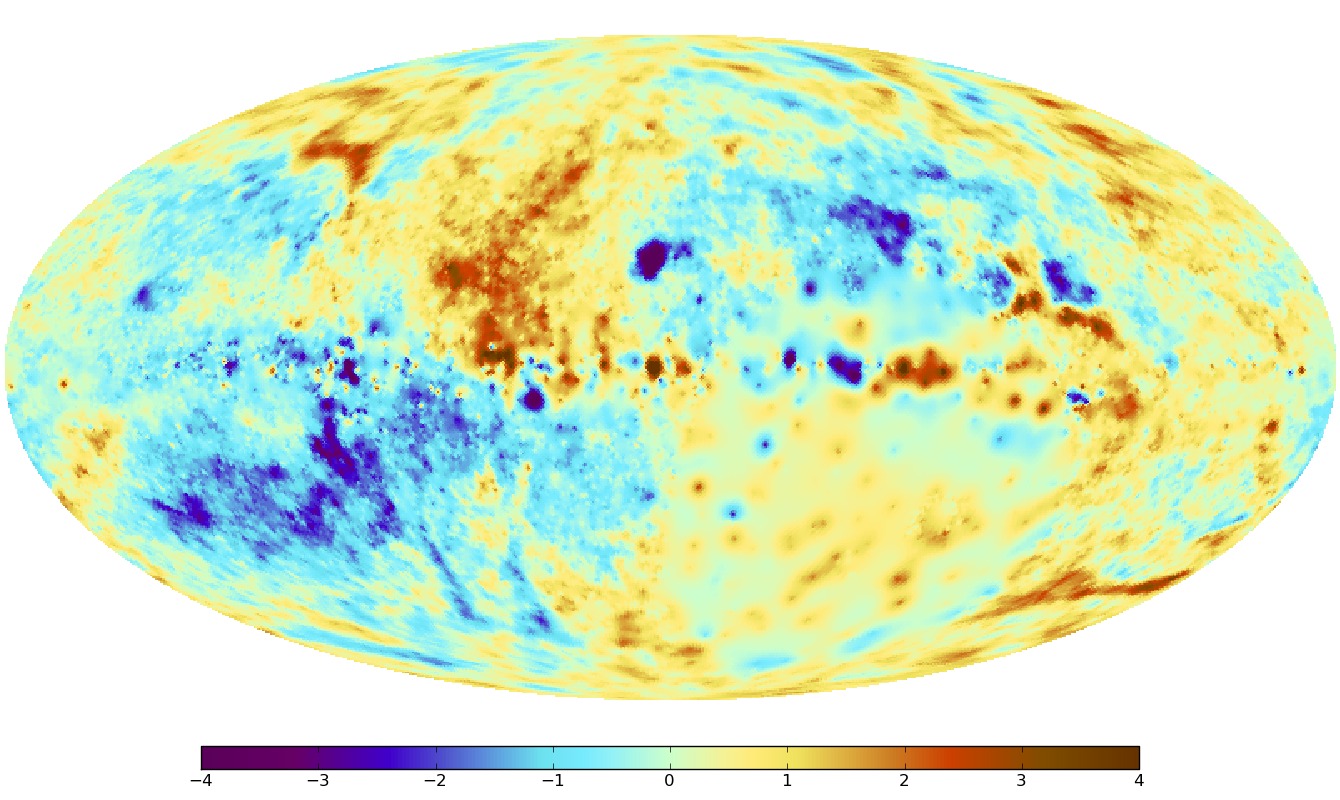
With a unique new all-sky map, scientists at MPA have made significant progress toward measuring the magnetic field structure of the Milky Way in unprecedented detail. Specifically, the map is of a quantity known as Faraday depth, which among other things, depends strongly on the magnetic fields along a particular line of sight. To produce the map, data were combined from more than 41,000 individual measurements using a novel image reconstruction technique. The work was a collaboration between scientists at the Max Planck Institute for Astrophysics (MPA), who are specialists in the new discipline of information field theory, and a large international team of radio astronomers. The new map not only reveals the structure of the galactic magnetic field on large scales, but also small-scale features that provide information about urbulence in the galactic gas.
D3PO: Denoising, Deconvolving, and Decomposing Photon Observations
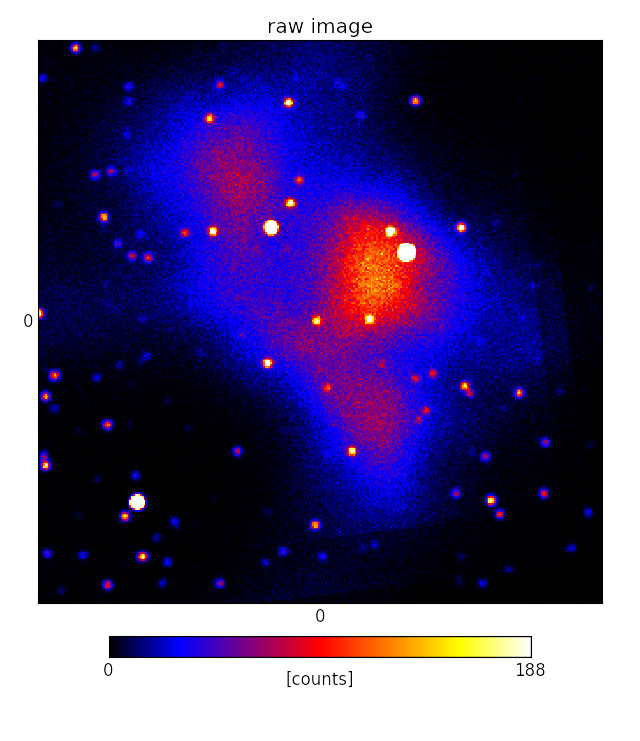
A common problem for scientists analysing astronomical images is the separation of diffuse and point-like components. This analysis has now become easier: scientists at the Max Planck Institute for Astrophysics have recently published the D3PO algorithm, which removes noise effects and instrumental artefacts from the observed images, while simultaneously separating diffuse and point-like contributions.
Resolving the radio sky
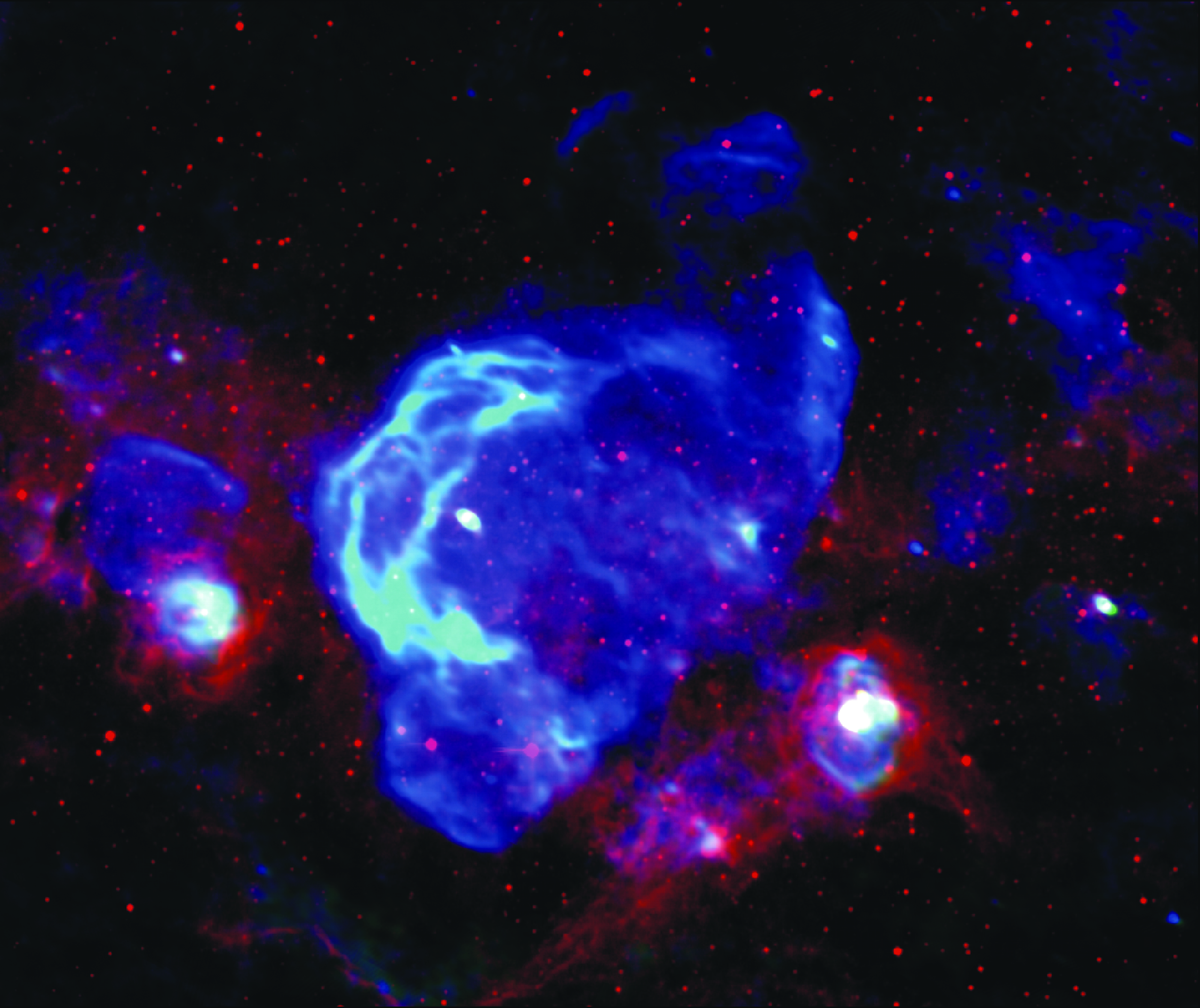
Radio astronomers obtain extremely high resolution sky images by using interferometers, instruments where several single radio telescopes are linked together. However, optimal data analysis procedures for such an instrument are significantly more involved than for a single telescope. Scientists from the Max Planck Institute for Astrophysics have now developed the algorithm RESOLVE which solves a number of outstanding problems in radio imaging.
Data analysis and steam engines

As astronomical telescopes become more and more sensitive, the analysis techniques become ever more sophisticated. But do we need a new theoretical approach for a modern image reconstruction method? Not necessarily, a well-known theory, originally developed for a better understanding of steam engines, does the trick: thermodynamics. Two researchers at the Max Planck Institute for Astrophysics have now shown that the so called Gibbs energy in thermodynamics, known for more than a century, can be applied to the development of new, optimal imaging techniques.
Mathematics of digital senses: Information Field Theory for signal recognition
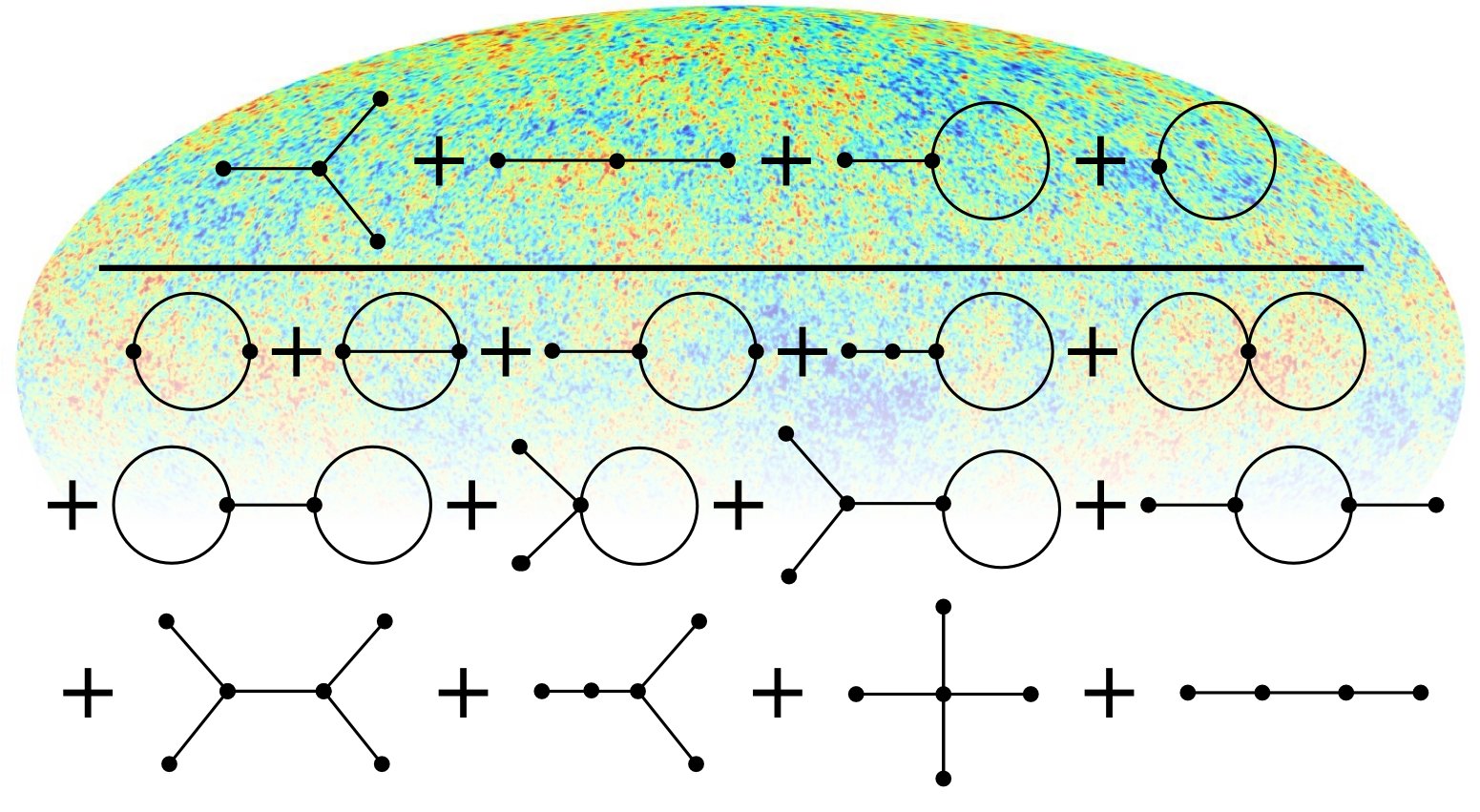
The correct interpretation of signals through our senses is not only an essential problem of living creatures, but also of fundamental scientific relevance. Scientists at the Max-Planck-Institute for Astrophysics have shown that mathematical methods from particle physics can be used for developing image reconstruction techniques. These yield optimal results even for incomplete, defective, and distorted data. Information Field Theory, which is used to develop such image reconstruction techniques, provides us with algorithms, i.e. mathematical instructions, for computing complicated perception processes in engineering and science, such as in cosmology.
IFT Introduction
-
Information Theory & Information Field Theory
University lectures by Torsten A. Enßlin (LMU Munich, 20.4.2020 - ), script, handouts, exercises, ... -
Information Field Theory: from astrophysical imaging to artificial intelligence
Talk by Torsten A. Enßlin at Joint Astronomical Colloquium (ESO Garching, 13.2.2020) - Information theory for fields
Torsten A. Enßlin, Annalen der Physik special issue on "Physics of Information" online article" arXiv:1804.03350 - Information field theory
Wikipedia - Why information field theory *is* a field theory
Torsten A. Enßlin, May 2015. link - Information field theory, an introduction in a nutshell
Torsten A. Enßlin, in MaxEnt 2012, the 32nd Workshop on Bayesian Inference and Maximum Entropy Methods in Science and Engineering, arXiv:1301.2556 - Astrophysical data analysis with information field theory, advanced recipes, also in a nutshell
Torsten A. Enßlin, accepted chapter to the conference proceedings for MaxEnt 2013, to be published by AIP, arXiv:1405.7701 - Bayesian Field Theory: Nonparametric Approaches to Density Estimation, Regression, Classification, and Inverse Quantum Problems
J. C. Lemm, arxiv:physics/9912005 and more of his works - Bayesian Field Theory applied to scattered data interpolation and inverse problems.
C. Farmer. Algorithms for Approximation, pages 147-166, 2007. eBook - A path-integral approach to Bayesian inference for inverse problems using the semiclassical approximation
Joshua C Chang, Van Savage, Tom Chou, J Stat Phys (2014) 157: 582 arXiv:1312.2974 - Information field theory for cosmological perturbation reconstruction and non-linear signal analysis
Torsten A. Enßlin, Mona Frommert, Francisco S. Kitaura 2009, Phys. Rev. D 80, 105005 arXiv:0806.3474 - IFT lecture notes and crash course notes
Theory
- Latent-space Field Tension for Astrophysical Component Detection
An application to X-ray imaging
Matteo Guardiani, Vincent Eberle, Margret Westerkamp, Julian Rüstig, Philipp Frank, Torsten Enßlin, submitted, arXiv:2506.20758 - Quantum Measurement and Objective Classical Reality
Vishal Johnson, Reimar Leike, Philipp Frank, Torsten A. Enßlin, Phys. Sci. Forum 2023, 9(1), 16; https://doi.org/10.3390/psf2023009016, arXiv:2309.02764 - Butterfly Transforms for Efficient Representation of Spatially Variant Point Spread Functions in Bayesian Imaging
Vincent Eberle, Philipp Frank, Julia Stadler, Silvan Streit, and Torsten A. Enßlin, Entropy 2023, 25(4), 652 https://doi.org/10.3390/e25040652 - Efficient Representations of Spatially Variant Point Spread Functions with Butterfly
Transforms in Bayesian Imaging Algorithms
Vincent Eberle, Philipp Frank, Julia Stadler, Silvan Streit, and Torsten A. Enßlin, Phys. Sci. Forum 2022, 5, 33. https://doi.org/10.3390/psf2022005033 - Measurement in a Unitary World
Vishal Johnson, Reimar Leike, Philipp Frank, Torsten A. Enßlin, arXiv:2212.03829 - Information Field Theory and Artificial Intelligence
Torsten A. Enßlin, Entropy 2022, 24, 374, arXiv:2112.10133 - Geometric Variational Inference
Philipp Frank, Reimar Leike, Torsten A. Enßlin, Entropy 2021, 23, 853, arXiv:2105.10470 - Towards Bayesian Data Compression
Johannes Harth-Kitzerow, Reimar Leike, Philipp Arras, Torsten A. Enßlin, Annalen der Physik 2021, Volume 533, 2000508, arXiv:2010.10375 - Bayesian Reasoning with Deep-Learned Knowledge
Jakob Knollmüller, Torsten A. Enßlin, 2021, Entropy 23, 693 arXiv:2001.11031 - Metric Gaussian Variational Inference
Jakob Knollmüller, Torsten A. Enßlin, submitted arXiv:1901.11033 - A Bayesian Model for Bivariate Causal Inference
Maximilian Kurthen, Torsten A. Enßlin, Entropy 2020, 22, 46; doi:10.3390/e22010046 arXiv:1812.09895 - Bayesian parameter estimation of miss-specified models
Johannes Oberpriller, Torsten A. Enßlin, submitted arXiv:1812.08194 - Encoding prior knowledge in the structure of the likelihood
Jakob Knollmüller, Torsten A. Enßlin, submitted arXiv:1812.04403 - Renormalization group computation of likelihood functions for cosmological data sets
Patrick McDonald, submitted arXiv:1810.08454 - Separating diffuse from point-like sources - a Bayesian approach
Jakob Knollmüller, Philipp Frank, Torsten A. Enßlin, submitted arXiv:1804.05591 - Inference of signals with unknown correlation structure from non-linear measurements
Jakob Knollmüller, Theo Steininger, Torsten A. Enßlin, submitted arXiv:1711.02955 - Towards information optimal simulation of partial differential equations
Reimar H. Leike, Torsten A. Enßlin, Physical Review E, Volume 97, Issue 3, id.033314 ePrint, arXiv:1709.02859 - Noisy independent component analysis of auto-correlated components
Jakob Knollmüller, Torsten A. Enßlin, Phys. Rev. E 96, 042114 (2017) arXiv:1705.02344 - Correlated signal inference by free energy exploration
Torsten A. Enßlin, Jakob Knollmüller, submitted arXiv:1612.08406 - Optimal Belief Approximation
Reimar Leike, Torsten A. Enßlin, Entropy 2017, 19, 402; doi:10.3390/e19080402 arxiv:1610.09018 - Operator Calculus for Information Field Theory
Reimar Leike, Torsten A. Enßlin, Physical Review E, Volume 94, Issue 5, id.053306 (2016) arxiv:1605.00660 - Signal inference with unknown response: calibration uncertainty renormalized estimator
Sebastian Dorn, Torsten A. Enßlin, Maksim Greiner, Marco Selig, Vanessa Boehm, PRE 91, 013311 (2015) arXiv:1410.6289 - Improving self-calibration
Torsten A. Enßlin, Henrik Junklewitz, Lars Winderling, Maksim Greiner, Marco Selig, 2014, PRE 90, id.043301 arXiv:1312.1349 - Reconstruction of Gaussian and log-normal fields with spectral smoothness
Niels Oppermann, Marco Selig, Michael R. Bell, Torsten A. Enßlin, 2013, Phys. Rev. E 87, 032136 arXiv:1210.6866 - Reconstructing signals from noisy data with unknown signal and noise covariances
Niels Oppermann, Georg Robbers, Torsten A. Enßlin, 2011, Physical Review E 84, 041118 arXiv:1107.2384 - Reconstruction of signals with unknown spectra in information field theory with parameter uncertainty
Torsten A. Enßlin, Mona Frommert 2011, Physical Review D 83, 105014 arXiv:1002.2928 - Inference with minimal Gibbs free energy in information field theory
Torsten A. Enßlin, Cornelius Weig 2010, Physical Review E 82, 051112 arXiv:1004.2868 and Comment on Paper and Reply to Comment - and more related papers
IFT Applications
- Bayesian Imaging of Interferometric Data from Polarized Electromagnetic Signals
Philipp Arras, Jakob Roth, Martin Reinecke, Richard A. Perley, Andrei Frolov, Rüdiger Westermann, Torsten A. Enßlin (2024), submitted arxiv:2504.00227 - Bayesian Multi-wavelength Imaging of the LMC SN1987A with SRG/eROSITA
Vincent Eberle, Matteo Guardiani, Margret Westerkamp, Philipp Frank, Michael Freyberg, Mara Salvato, Torsten A. Enßlin (2024), submitted arxiv:2410.14599 - Imaging the black hole shadow and extended jet of M87
Jong-Seo Kim, Hendrik Mueller, Aleksei S. Nikonov, Ru-Sen Lu, Jakob Knollmueller, Torsten A. Enßlin, Maciek Wielgus, Andrei P. Lobanov, (2024), submitted arxiv:2409.00540 - Towards a Field Based Bayesian Evidence Inference from Nested Sampling Data
Margret Westerkamp, Jakob Roth, Philipp Frank, Will Handley, Torsten A. Enßlin, (2024), Entropy 2024, 26(11), 930; https://doi.org/10.3390/e26110930, arxiv:2408.09889 - Bayesian self-calibration and imaging in Very Long Baseline Interferometry
Jong-Seo Kim, Aleksei S. Nikonov, Jakob Roth, Torsten A. Ensslin, Michael Janssen, Philipp Arras, Hendrik Mueller, Andrei P. Lobanov, (2024), accepted for Publication in A&A, arxiv:2407.14873 - Spatially Coherent 3D Distributions of HI and CO in the Milky Way
Laurin Söding, Gordian Edenhofer, Torsten A. Enßlin, Philipp Frank, Ralf Kissmann, Vo Hong Minh Phan, Andrés Ramírez, Hanieh Zhandinejad, Philipp Mertsch, (2024), submitted arxiv:2407.02859 - fast-resolve: Fast Bayesian Radio Interferometric Imaging
Jakob Roth, Philipp Frank, Hertzog L. Bester, Oleg M. Smirnov, Rüdiger Westermann, Torsten Enßlin, (2024), accepted by A&A arxiv:2406.09144 - Introducing LensCharm -- A charming Bayesian strong lensing reconstruction framework
Julian Rüstig, Matteo Guardiani, Jakob Roth, Philipp Frank, Torsten Enßlin (2024), A&A 682, A146 https://doi.org/10.1051/0004-6361/202348256 - Non-parametric Bayesian reconstruction of Galactic magnetic fields using Information Field Theory:
The inclusion of line-of-sight information in ultra-high energy cosmic ray backtracking
Alexandros Tsouros, Abhijit B. Bendre, Gordian Edenhofer, Torsten Enßlin, Philipp Frank, Michalis Mastorakis, Vasiliki Pavlidou, (2024), A&A, 690, A102 (2024), https://doi.org/10.1051/0004-6361/202449933, arxiv:2403.05531 - Inferring Evidence from Nested Sampling Data via Information Field Theory
Margret Westerkamp, Jakob Roth, Philipp Frank, Will Handley, Torsten Enßlin, Phys. Sci. Forum 2023, 9(1), 19; https://doi.org/10.3390/psf2023009019, arXiv:2312.1190 - A BRAIN Study to Tackle Image Analysis with Artificial Intelligence in the ALMA 2030 Era
Fabrizia Guglielmetti, Michele Delli Veneri, Ivano Baronchelli, Carmen Blanco, Andrea Dosi, Torsten Enßlin, Vishal Johnson, Giuseppe Longo, Jakob Roth, Felix Stoehr, and et al., Physical Sciences Forum 9, no. 1: 18. https://doi.org/10.3390/psf2023009018 - Resolving Horizon-Scale Dynamics of Sagittarius A*
Jakob Knollmüller, Philipp Arras, Torsten A. Enßlin, submitted, arXiv:2310.16889 - Spectroscopic analysis of hot, massive stars in large spectroscopic surveys with de-idealised models
Joachim M. Bestenlehner, Torsten A. Enßlin, Maria Bergemann, Paul A. Crowther, Maksim Greiner, Marco Selig, (2024), Monthly Notices of the Royal Astronomical Society, Volume 528, Issue 4, pp.6735-6750 https://doi.org/10.1093/mnras/stae298 arXiv:2309.06474 - Spectroscopic analysis of hot, massive stars in large spectroscopic surveys with de-idealized models
Julian Rüstig, Matteo Guardiani, Jakob Roth, Philipp Frank, Torsten Enßlin (2024), Monthly Notices of the Royal Astronomical Society, Volume 528, Issue 4, pp.6735-6750 https://doi.org/10.1093/mnras/stae298 - First spatio-spectral Bayesian imaging of SN1006 in X-ray
Margret Westerkamp, Vincent Eberle, Matteo Guardiani, Philipp Frank, Lukas Platz, Philipp Arras, Jakob Knollmüller, Julia Stadler, and Torsten A. Enßlin, submitted, arXiv:2308.09176 - A Parsec-Scale Galactic 3D Dust Map out to 1.25 kpc from the Sun
Gordian Edenhofer, Catherine Zucker, Philipp Frank, Andrew K. Saydjari, Joshua S. Speagle, Douglas Finkbeiner, and Torsten A. Enßlin, submitted, arXiv:2308.01295 - Bayesian radio interferometric imaging with direction-dependent calibration
Jakob Roth, Philipp Arras, Martin Reinecke, Richard A. Perley, Rüdiger Westermann, and Torsten A. Enßlin, accepted by Astronomy and Astrophysics, arXiv:2305.05489 - Disentangling the Faraday rotation sky
Sebastian Hutschenreuter, Marijke Haverkorn, Philipp Frank, Nergis C. Raycheva, Torsten A. Enßlin A. (2023), arXiv:2304.12350 - Reconstructing Galactic magnetic fields from local measurements for backtracking ultra-high-energy cosmic rays
Alexandros Tsouros, Gordian Edenhofer, Torsten Enßlin, Michalis Mastorakis, Vasiliki Pavlidou, submitted (2023) doi:10.48550/arXiv.2303.10099 - Bayesian Statistics Approach to Imaging of Aperture Synthesis Data: RESOLVE Meets ALMA
Łukasz Tychoniec, Fabrizia Guglielmetti, Philipp Arras, Torsten Enßlin, Eric Villard, Phys. Sci. Forum 2022, 5(1), 52; doi:10.3390/psf2022005052 - Fast-Cadence High-Contrast Imaging with Information Field Theory
Jakob Roth, Gianluca Li Causi, Vincenzo Testa, Philipp Arras, Torsten A. Enßlin (2022), Astronomical Journal 165, 86, doi:10.3847/1538-3881/acabc1, arXiv:2212.07714 - The Galactic 3D large-scale dust distribution via Gaussian process regression on spherical coordinates
Reimar H. Leike, Gordian Edenhofer, Jakob Knollmller, Christian Alig, Philipp Frank, Torsten A. Enßlin (2022), submitted, arXiv:2004.06732 - Multi-Component Imaging of the Fermi Gamma-ray Sky in the Spatio-spectral Domain
Platz, Lukas I. ; Knollmüller, Jakob ; Arras, Philipp ; Frank, Philipp ; Reinecke, Martin ; Jüstel, Dominik ; Enßlin, Torsten A. (2022), arXiv:2204.09360 - Variable structures in M87* from space, time and frequency resolved interferometry
Philipp Arras, Philipp Frank, Philipp Haim, Jakob Knollmüller, Reimar Leike, Martin Reinecke, Torsten A. Enßlin (2022), Nature Astronomy, https://doi.org/10.1038/s41550-021-01548-0 arXiv:2002.05218 - Deep Images of the Galactic Center with GRAVITY
Julia Stadler et al. (2021), A&A, Forthcoming article arXiv:2112.07477 - Studying Bioluminescence Flashes with the ANTARES Deep Sea Neutrino Telescope
Nico Reeb et al. (2023), Limnology and Oceanography Methods, Volume 21, Issue 11, pages 734-760, https://doi.org/10.1002/lom3.10578 arXiv:2107.08063 - Non-parametric Bayesian Causal Modeling of the SARS-CoV-2 Viral Load Distribution vs. Patient's Age
Matteo Gurdiani et al. (2021), arXiv:2105.13483 - The Galactic Faraday rotation sky 2020
Sebastian Hutschenreuter et al. (2021), arXiv:2102.01709 - Reconstructing non-repeating radio pulses with Information Field Theory
Christoph Welling, Philipp Frank, Torsten A. Enßlin, Anna Nelles (2021), arXiv:2102.00258 - Comparison of classical and Bayesian imaging in radio interferometry
Philipp Arras, Richard A. Perley, Hertzog L. Bester, Reimar Leike, Oleg Smirnov, Rüdiger Westermann, Torsten A. Enßlin (2020), arXiv:2008.11435 - Resolving nearby dust clouds
Reimar H. Leike, Martin Glatze, Torsten A. Enßlin (2020), Astronomy & Astrophysics, Volume 639, A138, 10.1051/0004-6361/202038169, arXiv:2004.06732 - Unified Radio Interferometric Calibration and Imaging with Joint Uncertainty Quantification
Philipp Arras, Philipp Frank, Reimar Leike, Rüdiger Westermann, Torsten A. Enßlin (2019), Astronomy & Astrophysics, Volume 627, id.A134, 12 pp. 10.1051/0004-6361/201935555; arXiv:1903.11169 - The Galactic Faraday depth sky revisited
Sebastian Hutschenreuter, Torsten A. Enßlin, Astronomy & Astrophysics, Volume 633, id.A150, 16 pp.d eJournal, arXiv:1903.06735 - Charting nearby dust clouds using Gaia data only
Reimar Leike, Torsten A. Enßlin, A&A 631, A32 (2019); doi:10.1051/0004-6361/201935093; arXiv:1901.05971 - The primordial magnetic field in our cosmic backyard
Sebastian Hutschenreuter, Sebastian Dorn, Jens Jasche, Franco Vazza, Daniela Paoletti, Guilhem Lavaux, Torsten A. Enßlin, Classical and Quantum Gravity, Volume 35, Issue 15, article id. 154001 (2018) DOI: 10.1088/1361-6382/aacde0 arXiv:1803.02629 - Radio Imaging With Information Field Theory
Philipp Arras, Jakob Knollmüller, Henrik Junklewitz, Torsten A. Enßlin, submitted arXiv:1803.02174 - Denoising, Deconvolving and Decomposing multi-Dimensional Photon Observations- The D4PO Algorithm
Daniel Pumpe, Martin Reinecke, Torsten A. Enßlin, Astronomy & Astrophysics 619 , 119 (2018) arXiv:1802.02013 - Inferring Galactic magnetic field model parameters using IMAGINE - An Interstellar MAGnetic field INference Engine
Theo Steininger, Torsten A. Enßlin, Maksim Greiner, Tess Jaffe, Ellert van der Velden, Jiaxin Wang, Marijke Haverkorn, Jörg R. Hörandel, Jens Jasche, Jörg P. Rachen, submitted arXiv:1801.04341 - Bayesian weak lensing tomography: Reconstructing the 3D large-scale distribution of matter with a lognormal prior
Vanessa Böhm, Stefan Hilbert, Maksim Greiner, Torsten A. Enßlin, Physical Review D, Volume 96, Issue 12, id.123510 arXiv:1701.01886 DOI - Search for quasi-periodic signals in magnetar giant flares
Daniel Pumpe, Michael Gabler, Theo Steininger, Torsten A. Enßlin, Astronomy & Astrophysics, Volume 610, id.A61, 12 pp. eJournal, arXiv:1708.05702 - Information Field Theory with INTEGRAL/SPI data
Mahsa Ghaempanah, Dissertation, LMU München: Faculty of Physics (2017) thesis - Cosmic expansion history from SN Ia data via information field theory
Natalia Porqueres, Torsten A. Enßlin, Maksim Greiner, Vanessa Boehm, Sebastian Dorn, Pilar Ruiz-Lapuente, Alberto Manrique, submitted arXiv:1608.04007 - Tomography of the Galactic free electron density with the Square Kilometer Array
Maksim Greiner, Dominic Schnitzeler, Torsten A. Enßlin, A&A 590, A59 (2016) arXiv:1512.03480 - Stochastic determination of matrix determinants
Sebastian Dorn, Torsten A. Enßlin, Phys. Rev. E 92, 013302 (2015) arXiv:1504.02661 - Using rotation measure grids to detect cosmological magnetic fields - a Bayesian approach
V. Vacca, N. Oppermann, T. Enßlin, J. Jasche, M. Selig, M. Greiner, H. Junklewitz, M. Reinecke, M. Brueggen, E. Carretti, L. Feretti, C. Ferrari, C. A. Hales, C. Horellou, S. Ideguchi, M. Johnston-Hollitt, R. F. Pizzo, H. Roettgering, T. W. Shimwell, K. Takahashi, A&A 591, A13 (2016) arXiv:1509.00747 - Estimating extragalactic Faraday rotation
Niels Oppermann, Henrik Junklewitz, Maksim Greiner, Torsten A. Enßlin, Takuya Akahori, Ettore Carretti, Bryan M. Gaensler, Ariel Goobar, Lisa Harvey-Smith, Melanie Johnston-Hollitt, Luke Pratley, Dominic H. F. M. Schnitzeler, Jeroen M. Stil, Valentina Vacca, (2015) A&A 575, id.A118, 25 arXiv:1404.3701 - A Bayesian method for pulsar template generation
M. Imgrund, D.J. Champion, M. Kramer, H. Lesch, MNRAS (June 01, 2015) 449 (4): 4162 arXiv:1501.03497 - All-sky reconstruction of the primordial scalar potential from WMAP temperature data
Sebastian Dorn, Maksim Greiner, Torsten A. Enßlin, JCAP02 (2015) 041 arXiv:1412.8315 data - The Denoised, Deconvolved, and Decomposed Fermi gamma-ray Sky - An Application of the D3PO Algorithm
Marco Selig, Valentina Vacca, Niels Oppermann, Torsten A. Enßlin, A&A 581, A126 (2015) arXiv:1410.4562 data - Log-transforming the matter power spectrum
Maksim Greiner, Torsten A. Enßlin, A&A 574, A86 (2015) arXiv:1312.1354 - Estimating extragalactic Faraday rotation
Niels Oppermann, Henrik Junklewitz, Maksim Greiner, Torsten A. Enßlin, Takuya Akahori, Ettore Carretti, Bryan M. Gaensler, Ariel Goobar, Lisa Harvey-Smith, Melanie Johnston-Hollitt, Luke Pratley, Dominic H. F. M. Schnitzeler, Jeroen M. Stil, Valentina Vacca, accepted ba A&A, arXiv:1404.3701 arXiv:1404.3701 data - A new approach to multi-frequency synthesis in radio interferometry
Henrik Junklewitz, Michael Bell, Marco Selig, Torsten A. Enßlin, Astronomy & Astrophysics, Volume 581, id.A5 (2015) arXiv:1401.4711 - RESOLVE: A new algorithm for aperture synthesis imaging of extended emission in radio astronomy
Henrik Junklewitz, Michael Bell, Marco Selig, Torsten A. Enßlin, A&A 586, A76 (2013), arXiv:1311.5282 - D3PO - Denoising, Deconvolving, and Decomposing Photon Observations
Marco Selig, Torsten A. Enßlin, accepted by Physical Review E, arXiv:1311.1888 arXiv:1311.1888 - A fast and precise way to calculate the posterior for the local non-Gaussianity parameter f_nl from Cosmic Microwave Background observations
Sebastian Dorn, Niels Oppermann, Rishi Khatri, Marco Selig, Torsten A. Enßlin, Phys. Rev. D 88, 103516 (2013) arXiv:1307.3884 - The XENON100 exclusion limit without considering Leff as a nuisance parameter
Jonathan H. Davis, Celine Boehm, Niels Oppermann, Torsten A. Enßlin, Thomas Lacroix, Physical Review D, vol. 86, Issue 1, id. 015027, 2012 arXiv:1203.6823 - An improved map of the Galactic Faraday sky
Niels Oppermann, et al., 2012, Astronomy & Astrophysics, Volume 542, id.A93 (2012) arXiv:1111.6186 - Improving stochastic estimates with inference methods: calculating matrix diagonals
Marco Selig, Niels Oppermann, Torsten A. Enßlin, Phys. Rev. E 85, 021134 (2012) arXiv:1108.0600 - Probing Magnetic Helicity with Synchrotron Radiation and Faraday Rotation
Niels Oppermann, Henrik Junklewitz, Georg Robbers, Torsten A. Enßlin 2011, Astronomy and Astrophysics, 530, id.A89 arXiv:1008.1246 - Bayesian analysis of spatially distorted cosmic signals from Poissonian data
Cornelius Weig, Torsten A. Enßlin 2010, MNRAS 409, 1393 arXiv:1003.1311 - Bayesian non-linear large scale structure inference of the Sloan Digital Sky Survey data release 7
Jens Jasche, Francisco S. Kitaura, Cheng Li, Torsten A. Enßlin 2010, MNRAS 409, 355 arXiv:0911.2498 - Fast Hamiltonian sampling for large-scale structure inference
Jens Jasche, Francisco S. Kitaura 2010, MNRAS 407, 29 arXiv:0911.2496 - Bayesian power-spectrum inference for Large Scale Structure data
Jens Jasche, Francisco S. Kitaura, Benjamin D. Wandelt, Torsten A. Enßlin 2010, MNRAS 406, 60 arXiv:0911.2493 - Cosmic Cartography of the Large-Scale Structure with Sloan Digital Sky Survey Data Release 6
Francisco S. Kitaura, Jens Jasche, Cheng Li, Torsten A. Enßlin, R.Benton Metcalf, Benjamin D. Wandelt, Gerard Lemson, Simon D.M. White 2009, MNRAS 400, 183 arXiv:0906.3978
Dynamics
- Analysis of Dynamical Field Inference in a Supersymmetric Theory
Margret Westerkamp, Igor Ovchinnikov, Philipp Frank, Torsten A. Enßlin, Phys. Sci. Forum 2022, 5(1), 27; https://doi.org/10.3390/psf2022005027 - Dynamical field inference and supersymmetry
Margret Westerkamp, Igor Ovchinnikov, Torsten A. Enßlin, Entropy 2021, 23(12), 1652; arXiv:2010.15414 - Probabilistic simulation of partial differential equations
Philipp Frank, Torsten A. Enßlin, 2020, submitted, arXiv:2010.06583 - Field dynamics inference for local and causal interactions
Philipp Frank, Reimar Leike, Torsten A. Enßlin, 2021, Annalen der Physik, 2000486, arXiv:1902.02624 - Towards information-optimal simulation of partial differential equations
Reimar Leike, Torsten A. Enßlin, 2018, Physical Review E, 97, 033314; journal article, arXiv:1709.02859 - Consistency and convergence of simulation schemes in Information field dynamics
Martin Dupont, Torsten A. Enßlin, 2018, Physical Review E, Vol. 98, No. 4, DOI: 10.1103/PhysRevE.98.043307, arXiv:1802.00971 - Field dynamics inference via spectral density estimation
Philipp Frank, Theo Steininger, Torsten A. Enßlin, Phys. Rev. E 96, 052104 (2017) arXiv:1708.05250 - Supersymmetric theory of stochastic ABC model
Igor Ovchinikov, Yuquan Sun, Torsten A. Enßlin and Kang L. Wang, J. Phys. Commun. (2018) doi.org/10.1088/2399-6528/aac94a - Dynamic system classifier
Daniel Pumpe, Maksim Greiner, Ewald Mueller, Torsten A. Enßlin, Physical Review E (Vol.94, No.1) DOI: 10.1103/PhysRevE.94.012132 arXiv:1601.07901 - Kinematic dynamo, supersymmetry breaking, and chaos
Igor Ovchinikov, Torsten A. Enßlin, Physical Review D, Volume 93, Issue 8, id.085023 (2016) arXiv:1512.01651 - Mathematical foundation of Information Field Dynamics
Christian Muench, master thesis, Technical University Munich arXiv:1412.1226 - Simulation of stochastic network dynamics via entropic matching
Tiago Ramalho, Marco Selig, Ulrich Gerland, Torsten A. Enßlin, Phys. Rev. E 87, 022719 (2013) arXiv:1209.3700 - Information field dynamics for simulation scheme construction
Torsten A. Enßlin, 2013, Phys. Rev. E 87, 013308 arXiv:1206.4229
IFT Tools
- J-UBIK:
- The JAX-accelerated Universal Bayesian Imaging Kit
Vincent Eberle, Matteo Guardiani, Margret Westerkamp, Philipp Frank, Julian Rüstig, Julia Stadler, Torsten A. Enßlin, submitted arXiv:2409.10381 - Numerical Information Field Theory
- Re-Envisioning Numerical Information Field Theory (NIFTy.re): A Library for Gaussian Processes and Variational Inference
Gordian Edenhofer, Philipp Frank, Jakob Roth, Reimar H. Leike, Massin Guerdi, Lukas I. Scheel-Platz, Matteo Guardiani, Vincent Eberle, Margret Westerkamp, Torsten A. Enßlin, submitted arXiv:2402.16683 - DENSe: Bayesian Density Estimation for Poisson Data. [ascl:2312.004]
- D3PO- Denoising, Deconvolving, and Decomposing Photon Observations
- Resolve- aperture synthesis imaging in radio interferomerty
- Charm- cosmic history agnostic reconstruction method
Further literature
- DIP -- Diagnostics for Insufficiencies of Posterior calculations in Bayesian signal inference
Sebastian Dorn, Niels Oppermann, Torsten A. Enßlin, Phy. Rev. E 88 arXiv:1307.3889 - Lectures on Probability, Entropy, and Statistical Physics
A. Caticha arXiv:0808.0012 - MAGIC: Exact Bayesian Covariance Estimation and Signal Reconstruction for Gaussian Random Fields
B. Wandelt arXiv:ph/0401623