| MPA-HOMEPAGE |
|
 |
Gravitational Waveform Catalog | ||
| |
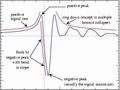 Go to:
|
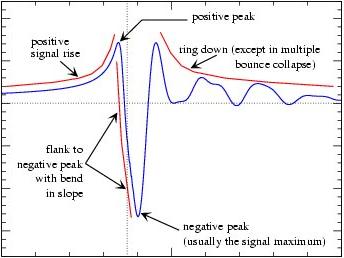 H. Dimmelmeier (
H. Dimmelmeier (J.A. Font ( H.-T. Janka A. Marek E. Müller C.D. Ott ( As a service to the scientific community, on this page we provide a waveform catalog of recent general relativistic numerical simulations of rotational core collapse. For details about the assumptions and approximations of the models, please go to the according simulation pages.
As more sophisticated simulations become available, we will add their
results to this page for download.
We have simulated a set of 136 rotational supernova core collapse models in axisymmetry. To simulate these models, we numerically solve the fully general relativistic hydrodynamic equations in a flux-conservative formulation [Banyuls, et al., 1997] on a grid using spherical coordinates. For an accurate resolution of shocks, we have implemented a modern high-resolution shock-capturing scheme, which uses characteristic information of relativistic hydrodynamics [Font, 2000]. The exact metric in the ADM spacetime foliation is approximated by assuming conformal flatness for the three-metric, which significantly reduces the complexity of the hydrodynamic and metric equations. As initial configuration we choose the presupernova stellar models e15a, e15b, e20a, e20b, s11.2, s15, s20, or s40 [Woosley, et al., 2002]. The progenitor models e15a, e15b, e20a, and e20b have an angular momentum distribution from stellar evolution calculations, while on the s11.2, s15, s20, and s40 models we impose rotation [Komatsu, et al., 1989a, Komatsu, et al., 1989b] with different rates and profiles. During core collapse, we utilize a microphysical equations of state specifically designed for supernova core collapse, either the one by Shen et al. (Shen EoS) [Shen, et al., 1998] or the one by Lattimer and Swesty (LS EoS) [Lattimer and Swesty, 1998]. To approximate the effects of neutrinos in the infall phase, a very efficient parametric deleptonization scheme is used [Liebendörfer, 2005]. A detailed description of the models and other interesting information can be found in a published article [Dimmelmeier, et al., 2008]. Figures of the waveforms for each model in EPS and JPG format:
We have simulated a set of 54 rotational supernova core collapse models in axisymmetry. To simulate these models, we numerically solve the fully general relativistic hydrodynamic equations in a flux-conservative formulation [Banyuls, et al., 1997] on a grid using spherical coordinates. For an accurate resolution of shocks, we have implemented a modern high-resolution shock-capturing scheme, which uses characteristic information of relativistic hydrodynamics [Font, 2000]. The exact metric in the ADM spacetime foliation is approximated by assuming conformal flatness for the three-metric, which significantly reduces the complexity of the hydrodynamic and metric equations. As initial configuration we choose the presupernova stellar model s20 [Woosley, et al., 2002], on which we impose rotation [Komatsu, et al., 1989a, Komatsu, et al., 1989b] with different rates and profiles. During core collapse, we utilize a microphysical equation of state [Shen, et al., 1998] specifically designed for supernova core collapse. To approximate the effects of neutrinos in the infall phase, a very efficient parametric deleptonization scheme is used [Liebendörfer, 2005]. A detailed description of the models and other interesting information can be found in a published article [Dimmelmeier, et al., 2007]. Figures of the waveforms for each model in EPS and JPG format:
We have simulated a set of 26 rotational supernova core collapse models in axisymmetry. To simulate these models, we numerically solve the fully general relativistic hydrodynamic equations in a flux-conservative formulation [Banyuls, et al., 1997] on a grid using spherical coordinates. For an accurate resolution of shocks, we have implemented a modern high-resolution shock-capturing scheme, which uses characteristic information of relativistic hydrodynamics [Font, 2000]. The exact metric in the ADM spacetime foliation is approximated by assuming conformal flatness for the three-metric, which significantly reduces the complexity of the hydrodynamic and metric equations. The initial configurations are rotating 4/3-polytropes in equilibrium with a central density of rhoc ini = 1010 g/cm3 constructed by numerically solving the hydrodynamic equilibrium equations in a general relativistic spacetime [Komatsu, et al., 1989a, Komatsu, et al., 1989b]. The initial state is completely determined by the central density, the rotation rate betarot ini = Erot ini / Epot ini, and the rotation parameter A, which specifies the degree of differential rotation. The equation of state during core collapse consists of a polytropic and a thermal contribution. The collapse is initiated by reducing the adiabatic exponent gamma1. For densities rho > 2.0 . 1014 g/cm3, the adiabatic exponent is set to gamma1 = 2.5 mimicking the stiffening of the equation of state above nuclear matter density. We have also simulated one model with a soft supranuclear equation of state with gamma1 = 2.0. A detailed description of the models and other interesting information can be found in a series of published articles [Dimmelmeier, et al., 2001, Dimmelmeier, et al., 2002a, Dimmelmeier, et al., 2002b].
|