Binary evolution
I am studying the evolution of massive stars
(those that are the progenitors
of neutron stars and black holes) in binaries.
I'm focusing on the binaries evolving in isolation, so in environments where the
dynamical interactions with other stars or systems can be neglected
(unlike in dense stellar systems e.g. globular clusters).
In contrast to single stars, those that are bound in binaries can interact with their
companion stars; e.g. accrete or transfer the mass to its companion,
even merge with the other star. Those interactions strongly affect their evolution.
In my studies I've been using the population synthesis technique complemented
with the constraints imposed by the current observations.
Binaries are common
(
observational studies show that even 70 %
of massive stars have a companion that is close enough to have impact on their evolution)
and hence understanding the processes happening in binaries is important!
Compact binaries, double neutron stars
I'm particularly interested in the evolution of binaries that are the progenitors of double compact objects (DCO) - binaries composed of two end products of stellar evolution (neutron stars or black holes in case of massive stars) that are one of the main astrophysical sources of gravitational waves that can be observed with the detectors like LIGO/Virgo.Part of my research was devoted to the formation of double neutron stars (DNS; binaries composed of two neutron stars). In contrast to other types of DCOs, several DNS have been observed in our Galaxy, which makes it possible to contrast the theoretical models with observations (as we did e.g. here, having a closer look at the assumptions about the natal kick velocities gained by neutron stars at their formation commonly made in theoretical studies).
In this paper we discussed the impact of assumptions about various poorly constrained (both observationally and theoretically) stages of evolution of the DNS progenitors on the efficiency of formation of merging double neutron stars - i.e. on the number of DNS that can merge within the time corresponding to the age of the Universe that is expected to form per unit of mass formed in stars. We discussed the resulting differences in the merger rates of those systems, focusing on the local Universe (that is within the reach of the current network of gravitational wave detectors).
The data for the main simulated models discussed in this paper is available on the Synthetic Universe website (under download -> double compact objects -> Chruslinska et al. 2018)
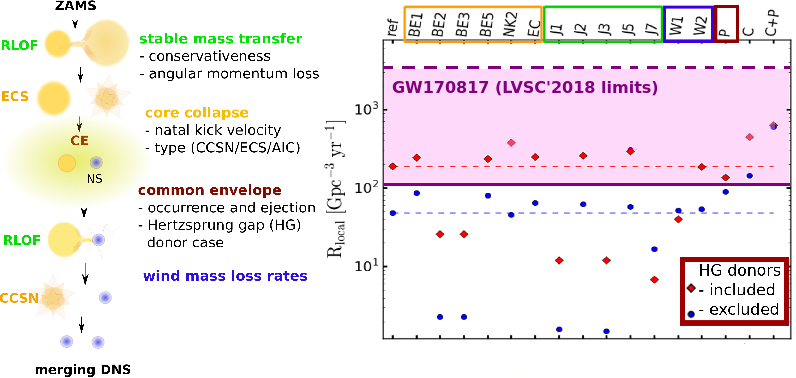
Updated figure from my IAU proceedings paper: summary of the main stages of evolution of a binary that leads to the formation of a merging double neutron star system. To simulate this evolutionary path, we need to make a number assumptions about all of those stages (the main factors are listed in the figure). Different assumptions lead to differences e.g. in the estimated local merger rate density, as shown on the right for the models discussed in Chruslinska et al. (2018). Note that the comparison shown in the figure assumes a particular star formation history and chemical evolution of the Universe and does not take into account the associated uncertainties.
Compact binaries & gravitational waves
Gravitational wave observations begin to probe the properties of the populations of merging double compact objects, such as their mass distribution and the frequency of mergers. They provide observational constraints on those properties that can be confronted with theoretical models and help to validate the assumptions about the evolution of their progenitor systems. However, this comparison is not straightforward!
Merger rate density: theoretical estimates & uncertainties
To estimate the merger rate densities (and other properties) of double compact objects one needs to combine the information about the environment in which the progenitors of the merging stellar remnants have formed (this could have been really long time ago!), initial parameters of the progenitor binary (e.g. masses, separation) and about the evolution of massive stars in binaries (e.g. how they interact, how much mass they lose, how and what stellar remnants they form). All of those assumptions contribute to the uncertainty of the final result. We need to understand the uncertainties coming from all of them to be able to correctly compare the theoretical estimates with observations!I am involved in studying the impact of all of those assumptions on the properties of merging DCO.
Papers related to my work in that topic:
- binary evolution related uncertainties (for double neutron stars) Chruslinska et al. (2018)
- uncertainties related to the distributions of initial binary parameters Klencki et al. (2018)
- the impact of the assumed distribution of the cosmic star formation rate density over metallicities and time (i.e. about the environment in which the DCO progenitors form) Chruslinska et al. (2019), Chruslinska & Nelemans (2019)
Binaries that we observe merging in the local Universe have formed some time ago
(needed for the two massive binary components to complete their evolution,
form two compact objects on a close orbit and decrease the orbital separation
of the binary due to gravitational waves emission up to the point when they merge)
from the matter with metallicity that was typical for their surroundings at that time.
DCOs form with different parameters and they need different amount of time to merge.
Our gravitational wave detectors observe a mixture of stars that formed a different
times in the cosmic history and in different environments.
background image used in the animation: http://misistemasolar.com/expansion-del-universo/
The importance of metallicity
The efficiency of formation of DCOs of different types depends on metallicity and this dependence is different for different DCOs. For instance, merging double black holes are found to form much more efficiently at low metallicities, while merging double neutron stars seem to show a much weaker dependence on metallicity (but note that this depends on the assumed evolutionary model!). This means that the assumptions about the fraction of stars forming at different metallicities and times (SFR(Z, t); those assumptions can differ significantly across the literature!) affect the merger rate estimates and they affect the estimates for different DCOs differently (i.e. affect the ratio of rates for different DCOs). We discuss that in this paper. This highlights the importance of finding tighter constraints on SFR(Z, t) and understanding the associated uncertainties.
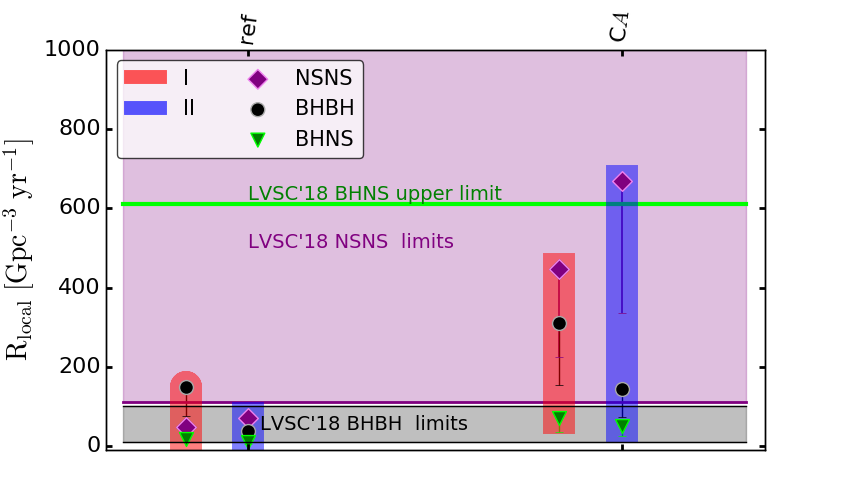
Updated figure from Chruslinska et al. (2019) which shows how the local merger rate density for different DCO types (purple diamonds -- double neutron stars, black circles -- double black holes, green triangles -- black hole - neutron star systems) changes when the assumptions about the fraction of stars forming at different metallicities at different times in the cosmic history are changed. The points within the red bins are the rate estimates that assume that even in the local Universe the majority of stars forms at metallicities smaller than solar. The points within the blue bins are the rates calculated under the assumption that the birth metallicity of stars forming at different times is substantially higher than in the 'red case'. The red and blue bins on the left share the same population synthesis model (set of assumptions about the binary evolution, 'ref') and the bins on the right correspond to other example population synthesis model ('CA'). The 'errorbars' show how the rate estimates would change if different distributions of initial binary parameters (resulting from the recent observational studies) were used (i.e. the rate estimates would be lower - the points would move towards the lower end of the errorbar). The green line, purple area and black area show the O2 LIGO/Virgo observational limits on the local merger rate density of neutron star - black hole (upper limit), double neutron star and double black hole systems respectively.
Chemical evolution
of the Universe
...why should I care ?
(here is example why for those interested in stellar/binary evolution and the outcome thereof/transients!/)Metallicity is one of the crucial factors that determine stellar evolution. To characterize the properties of stellar populations one needs to know the fraction of stars forming at different metallicities. Knowing how this fraction evolves over time is necessary e.g. to estimate the rates of occurrence of any stellar evolution related phenomena e.g. double compact object mergers, different types of supernovae. This is particularly important for the transients whose formation is highly sensitive to metallicity, such as long gamma ray bursts and double black hole mergers.
To compare the theoretical estimates of the rates with the observational limits, one also needs to know the uncertainty associated with the distribution of the cosmic star formation rate density at different metallicities and time (or redshift).
Observation-based picture & uncertainties
We set ourselves a goal of finding the observation-based answer to the question:- how does the distribution of the cosmic star formation rate density at different metallicities and time (redshift) look like
- how uncertain it is according to current observations.
To find the answer, we combined the empirical scaling relations
(and some other observational properties) of the star forming galaxies.
We address the question of uncertainty of the obtained distribution due to currently
unresolved observational issues, such as the absolute metallicity scale,
the flattening in the star formation-mass relation or the low mass end of the galaxy mass function.
See this paper
for the full story!
You can find the results of our calculations for all the cases discussed in the paper,
as well as some scripts to visualize the data
here.
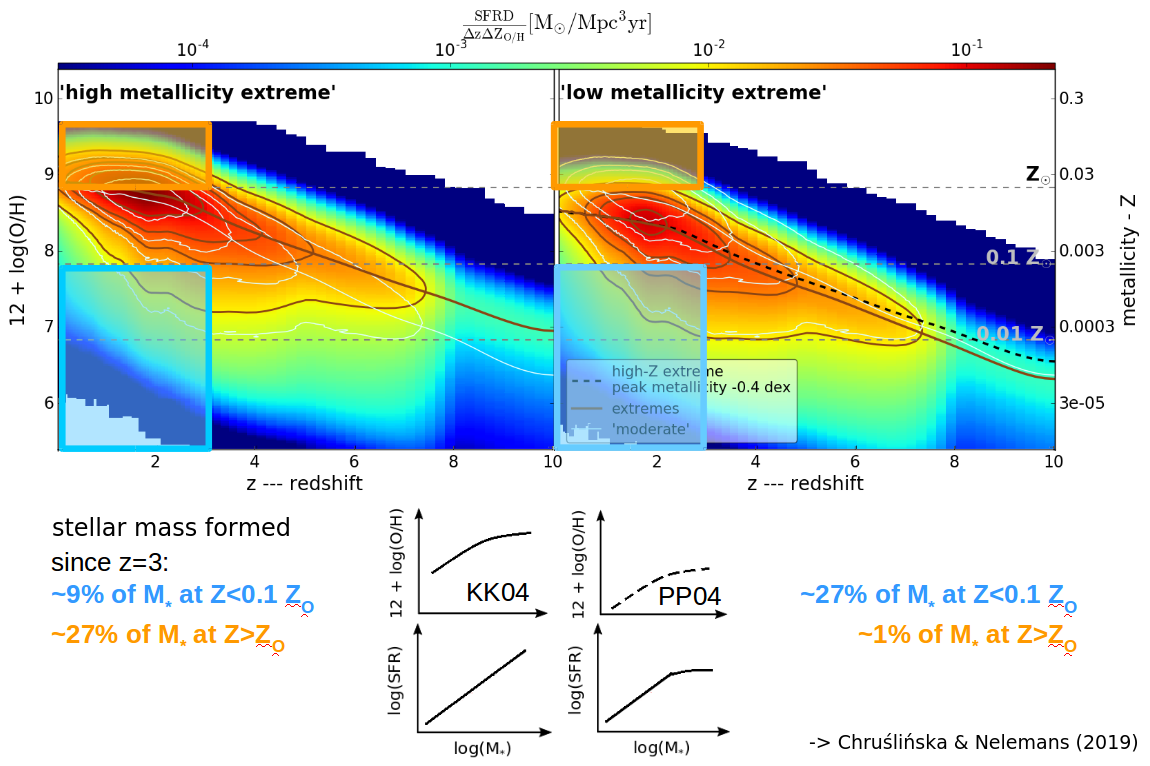
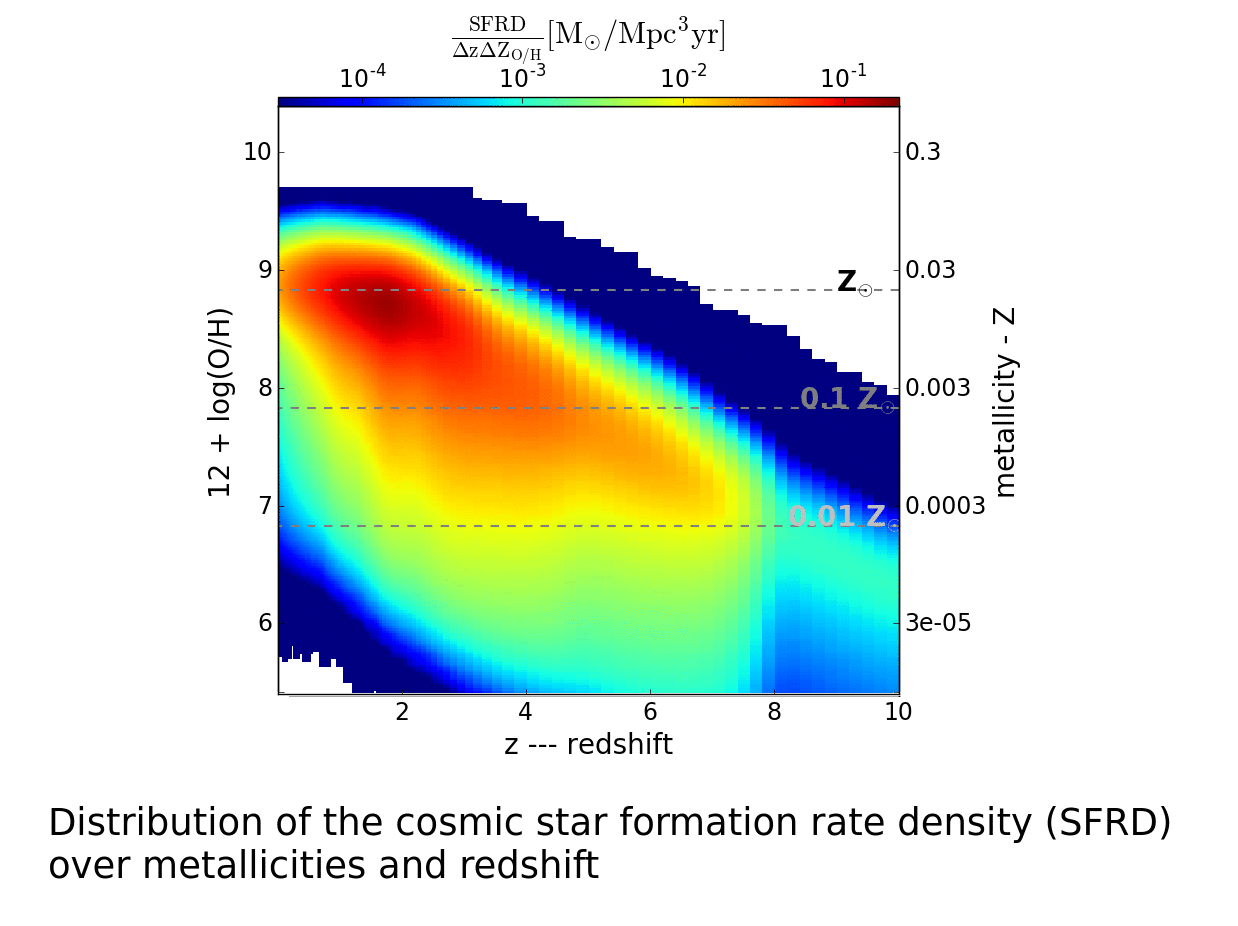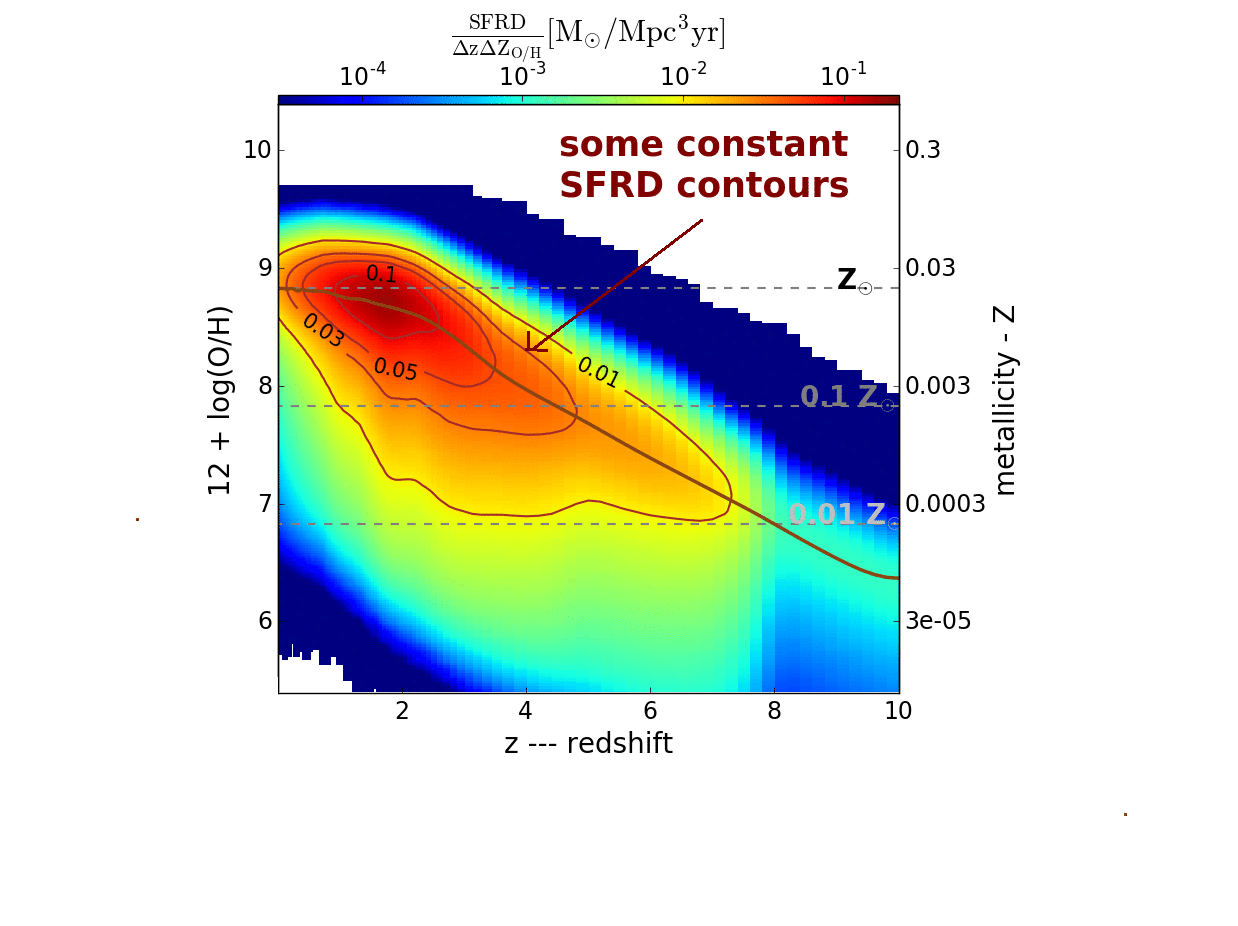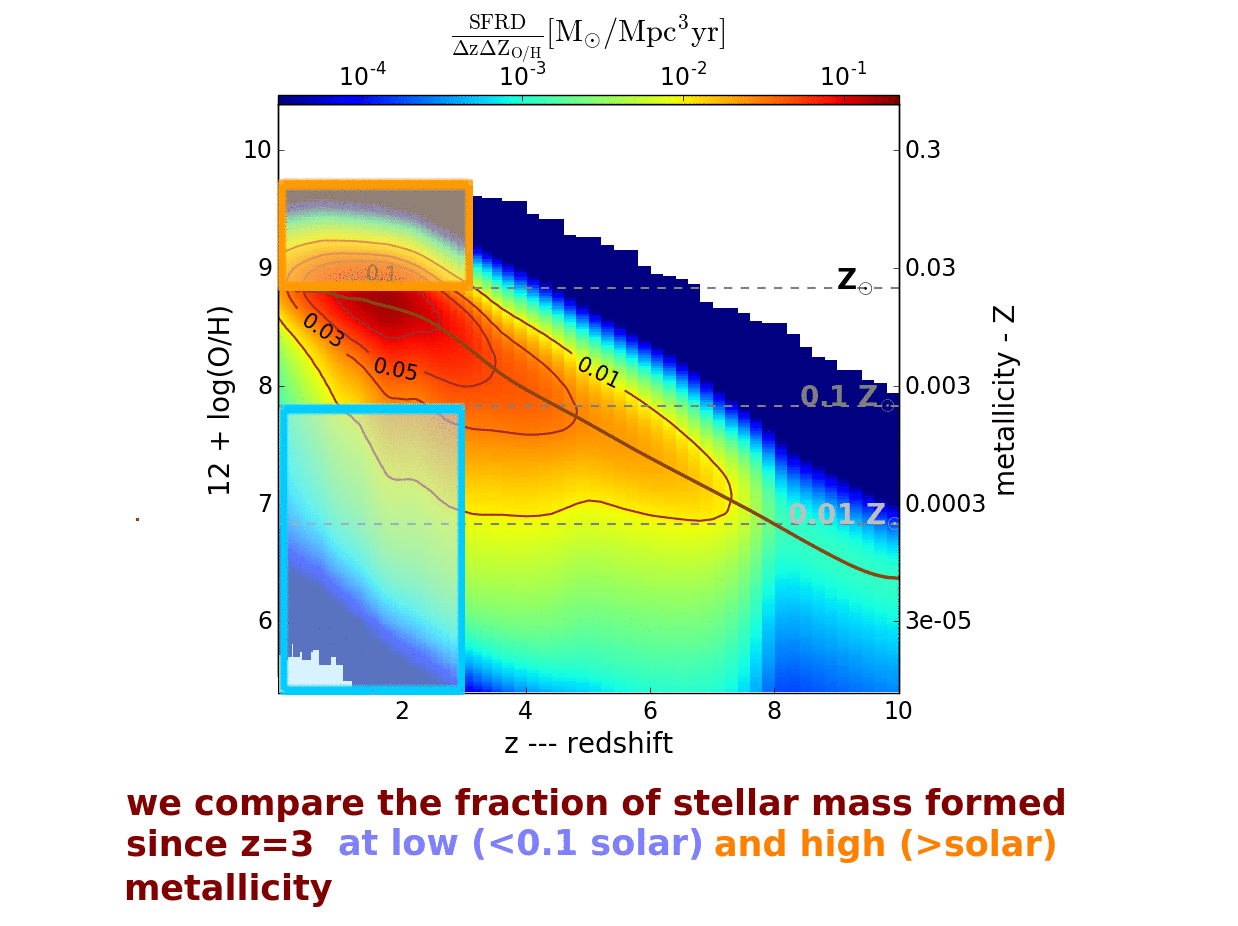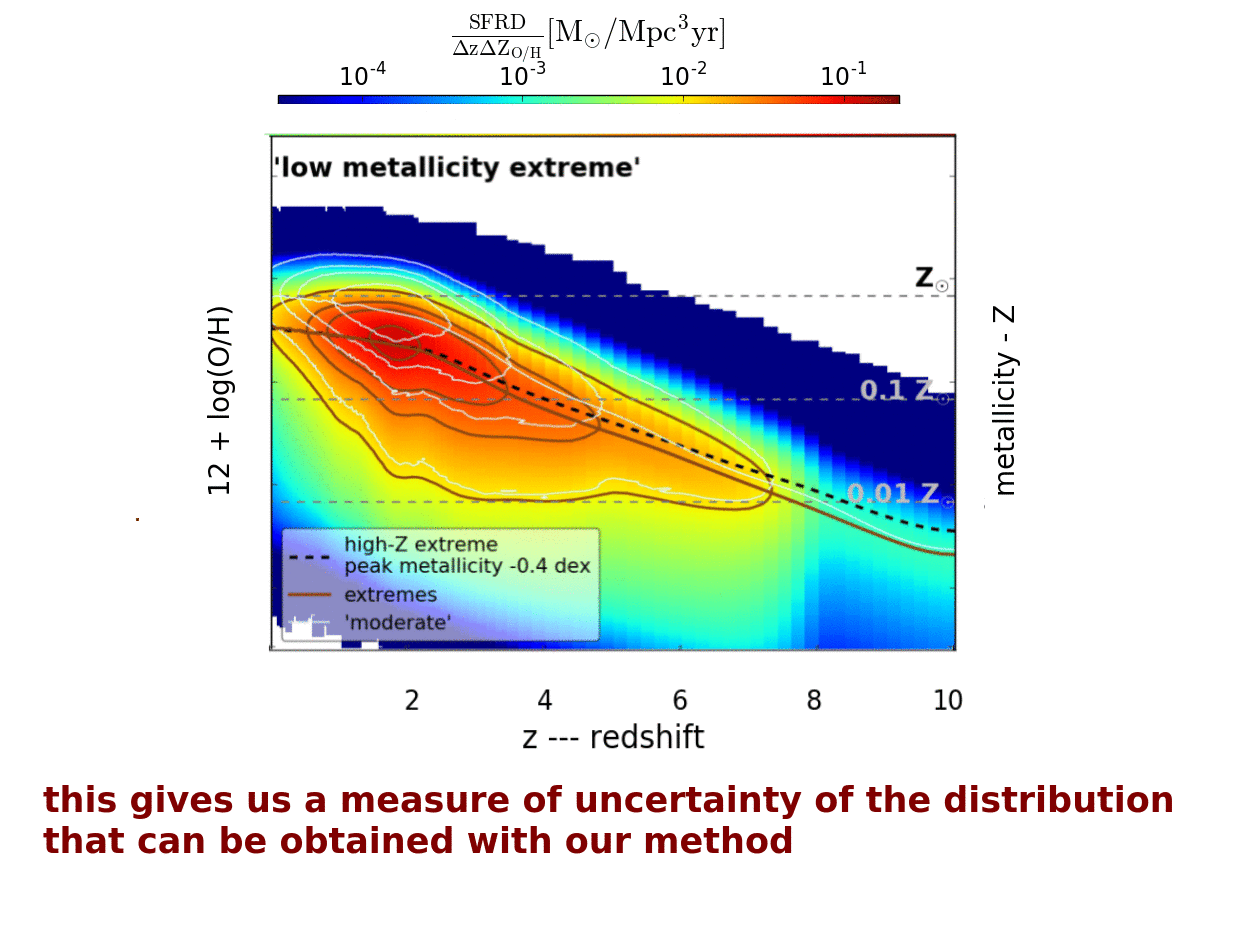
Modified figure from Chruslinska & Nelemans (2019)
that summarizes our main result.
It shows the distribution of the cosmic star formation rate density over metallicities and redshifts for the two variations −
the high and low metallicity extremes − that maximize the fraction of stellar mass formed at high and low metallicity respectively.
The difference between the two images delineates the uncertainty of the distribution obtained based on the observational
properties of star forming galaxies.
The fraction of stellar mass formed since z=3 at low (below 10% solar -- within the blue rectangle) and
high (above solar -- within the orange rectangle) metallicity differs between the two extremes by ~18 % and ~26 %
respectively.
The colour indicates the star formation rate density - most of the stellar mass forms in the red part of
the metallicity - redshift plane. Note that the brown thick line (showing the peak metallicity of the
distribution at a given redshift) is ~0.4 dex lower in the low-metallicity extreme at redshifts below 3
and this difference increases at higher redshifts.
However, at these redshifts our results need to rely on extrapolations, where the mass-metallicity relation is
not constrained by observations.
The right metallicity scale (metal mass fraction Z) was obtained from the oxygen to hydrogen abundance ratios
(left scale; this is the quantity used as a measure of metallicity in the observational studies that we used)
assuming Anders & Grevesse (1989) solar metallicity and solar abundance ratios.
How to read those figures?
What if the IMF is not universal?
Recent observational and theoretical studies indicate that the stellar initial mass function (IMF) varies systematically with the environment (SFR, metallicity; great talk about this topic was recently given by Tereza Jerabkova and Andrew Hopkins ). Although the exact dependence of the IMF on those properties is likely to change with the improving observational constraints , the reported trend in the shape of the IMF appears robust: in high SFR/low metallicity environments the IMF is more top heavy (i.e. implies more massive stars) and in low SFR environments the IMF appears top light (i.e. implies less massive stars ) than the IMF estimated in the Milky Way. Such systematic variations may have non trivial effect on the inferred distribution of the cosmic SFRD over metallicity and redshift. This effect will also be different for stars of different masses. We discuss that in Chruslinska et al. (2020)
We apply the empirically driven model of IMF variations described by the integrated galactic IMF (IGIMF) theory as presented in Jerabkova et al. (2018) and revise the cosmic SFRD distribution over metallicity and redshift that was obtained under the assumption of a universal IMF by Chruslinska & Nelemans (2019).
What does it mean for merging double compact objects? A short answer is: probably not much ( but...)
[Flatter high mass slope of the IMF does not imply that there are more BH progenitors! see also Klencki et al. (2018)]
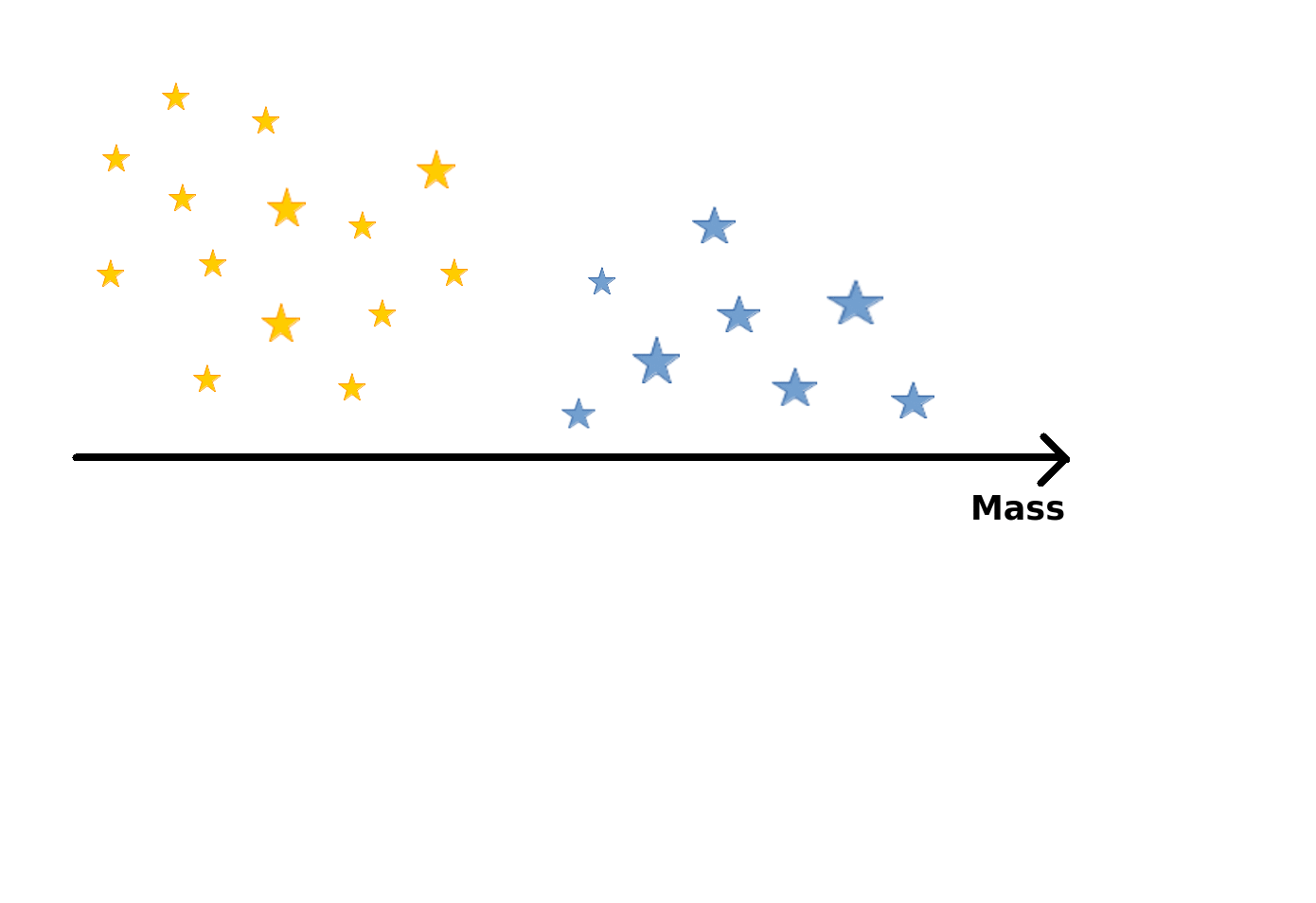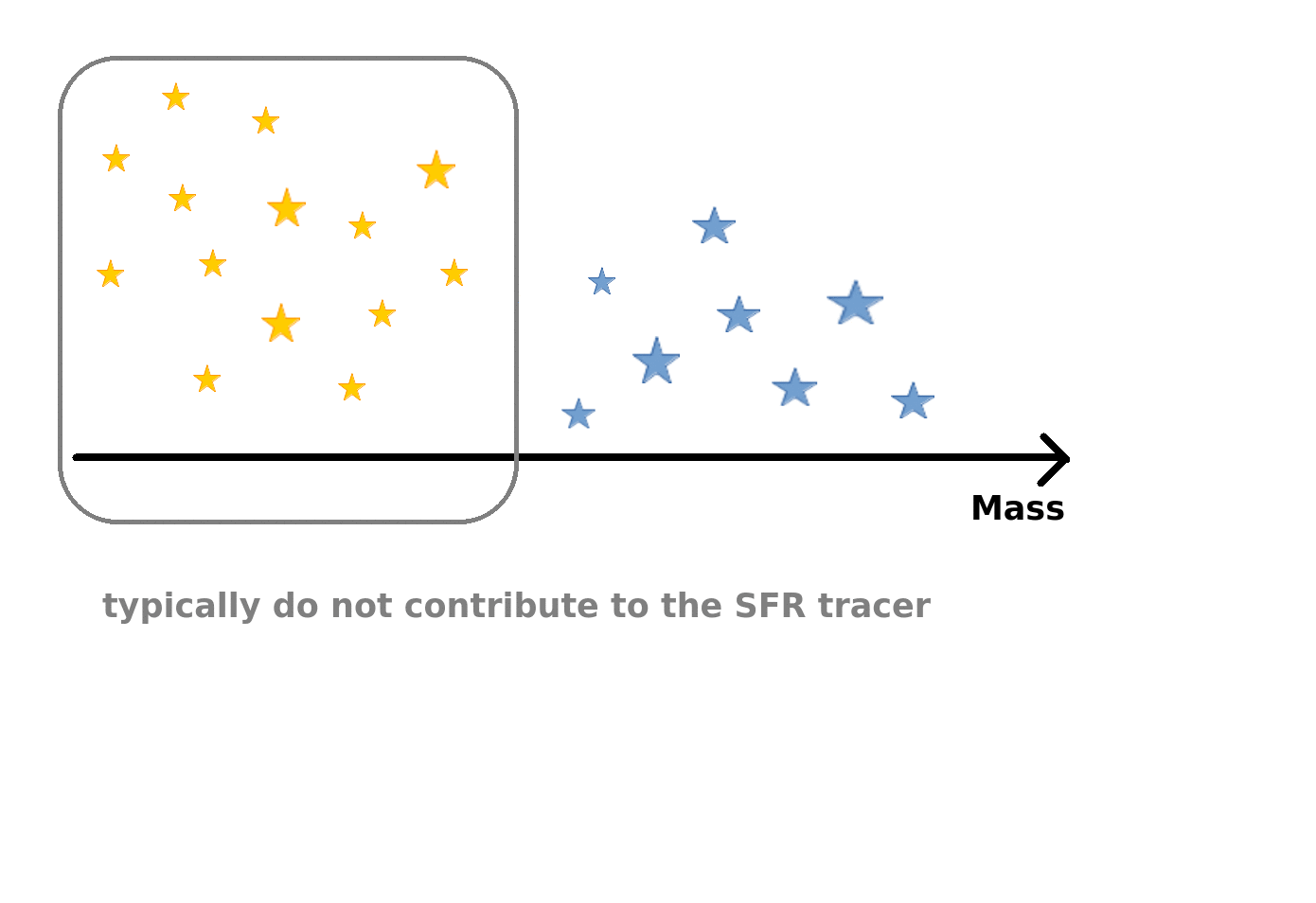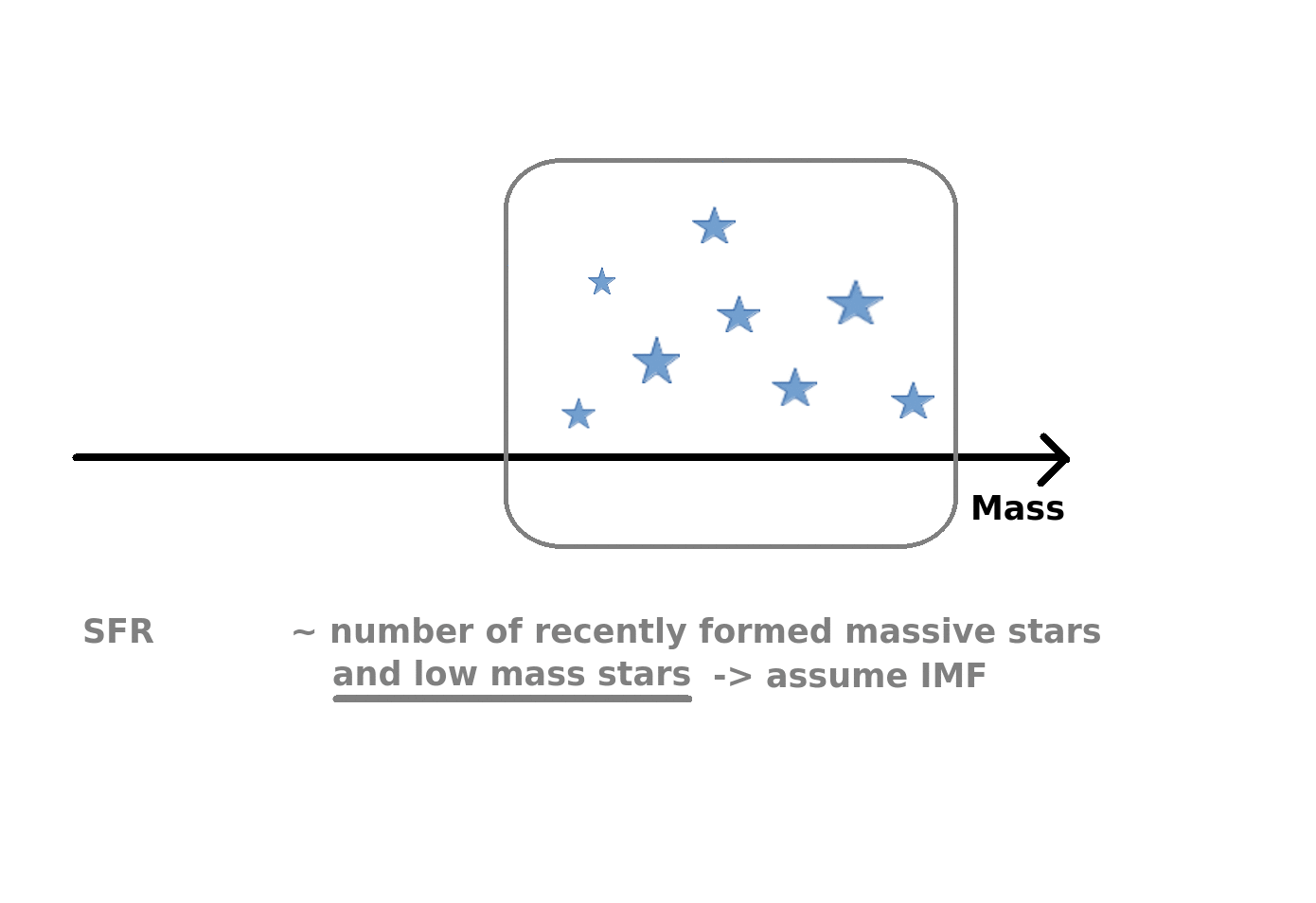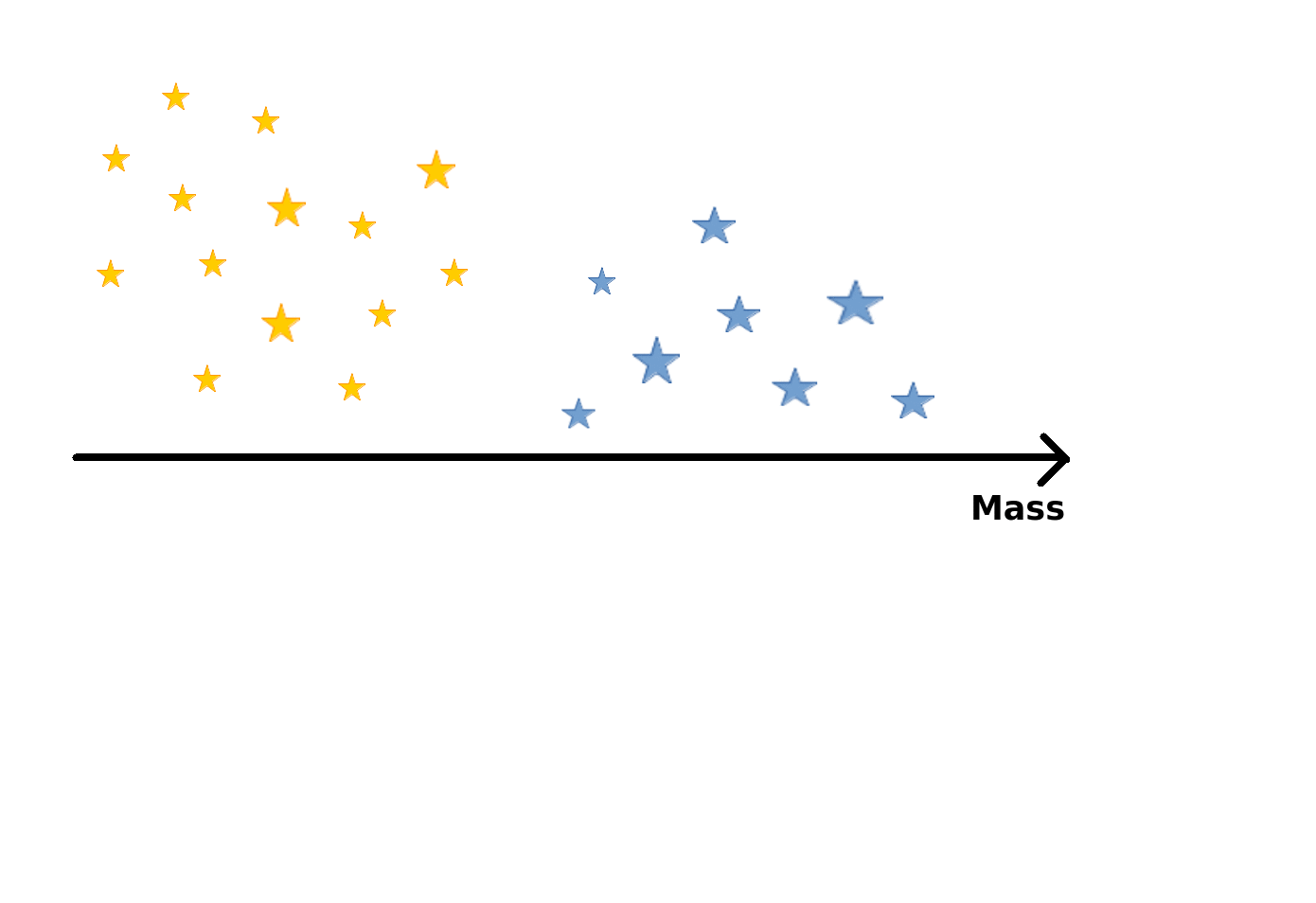
This is because the observational SFR estimates are based on the light that comes from massive stars and to account for the mass formd in stars that are not seen in the SFR tracer, one needs to assume a IMF -- so the two are not independent! When the SFR and IMF are varied consistently, the effect on the formation of BH progenitors is negligible. For NS progenitors the effect is rather small, but can potentially be important if there is a strong metallicity dependence in the formation of GW sources with NS. However, if you are interested in the properties of SN Ia progenitors, then the IMF variations may be something to keep in mind!
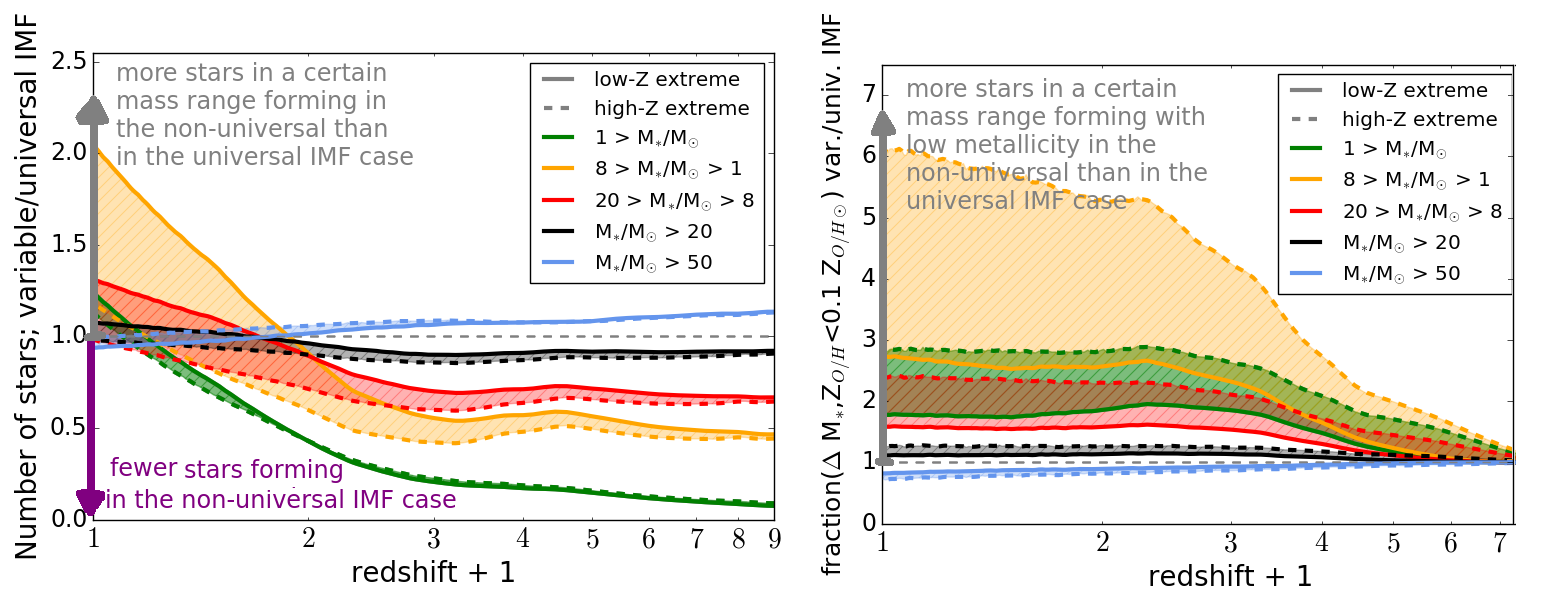
Modified figure from Chruslinska et al. 2020
Left: ratio of the number of stars forming in different mass ranges using the environment-dependent IMF to that
obtained using the universal IMF, as a function of redshift.
Right: ratio of the fraction of stars forming at low metallicity (below 0.1 solar) in different mass ranges
using the environment-dependent IMF to that obtained using the universal IMF, as a function of redshift.
At redshift z=1, about 2.5 times more stars with masses below 1 solar mass form at low metallicity in the considered
non universal IMF scenario.
We stress that the exact form of the IMF dependence on SFR and metallicity is likely to be further elucidated with improving empirical constraints, especially at higher redshifts and only the trends are robust. Therefore our study should be treated as a qualitative discussion of the expected impact of the assumptions regarding the (non)universality of the IMF on the distribution of the cosmic SFR over metallicity and redshift and the formation of stars in various mass ranges rather than a robust quantitative estimation of this effect. Our study provides guidance as to whether various calculations performed under the assumption of the universal IMF, e.g. estimates of the rates of different stellar-evolution-related phenomena (such as various types of SNe) are likely to under- or over-predict the estimated quantity and provides clues about the order of magnitude of this effect.