Highlights

Manipulative communication in humans and machines

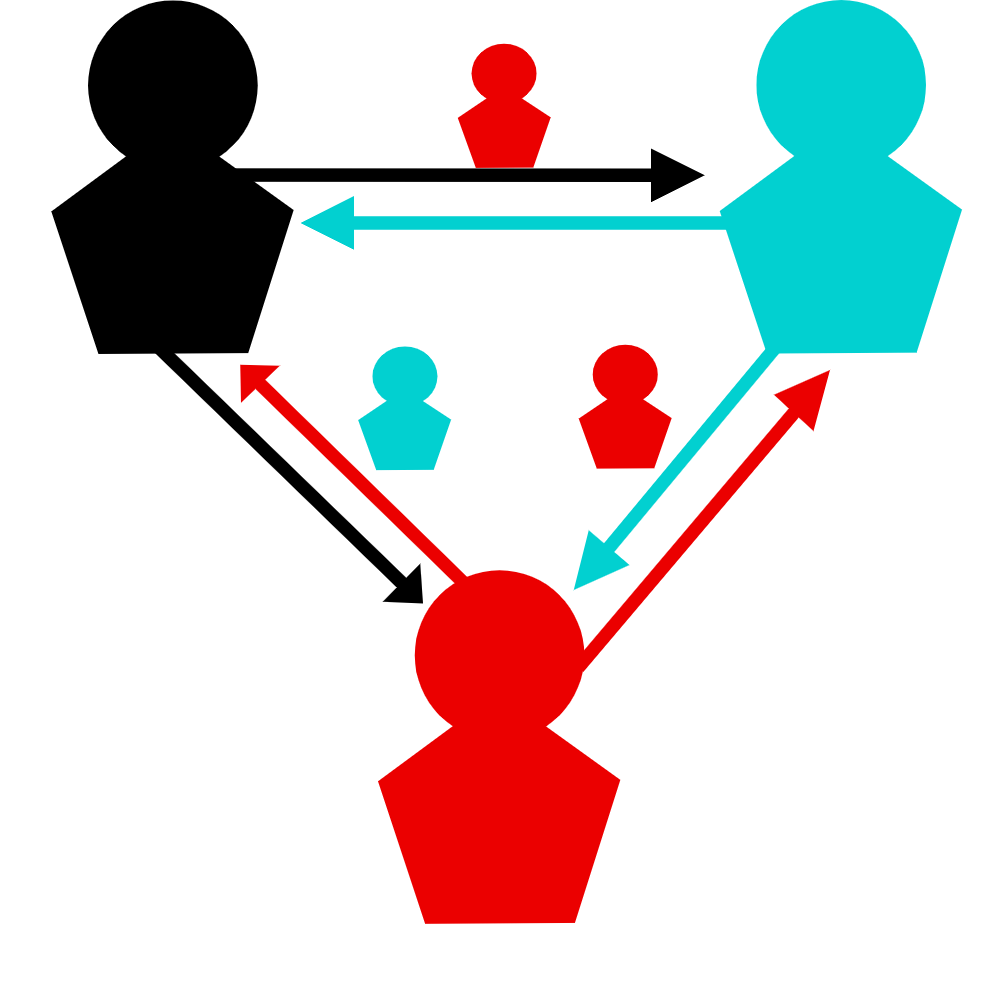
A universal sign of higher intelligence is communication. However, not all communications are well-intentioned. How can an intelligent system recognise the truthfulness of information and defend against attempts to deceive? How can a egoistic intelligence subvert such defences? What phenomena arise in the interplay of deception and defence? To answer such questions, researchers at the Max Planck Institute for Astrophysics in Garching, the University of Sydney and the Leibniz-Institut für Wissensmedien in Tübingen have studied the social interaction of artificial intelligences and observed very human behaviour.

• Learn more

Artificial intelligence combined



Artificial intelligence expands into all areas of the daily life, including research. Neural networks learn to solve complex tasks by training them on the basis of enormous amounts of examples. Researchers at the Max Planck Institute for Astrophysics in Garching have now succeeded in combining several networks, each one specializing in a different task, to jointly solve tasks using Bayesian logic in areas none was originally trained on. This enables the recycling of expensively trained networks and is an important step towards universally deductive artificial intelligence.

• Learn more

The embarrassment of false predictions -
How to best communicate probabilities?



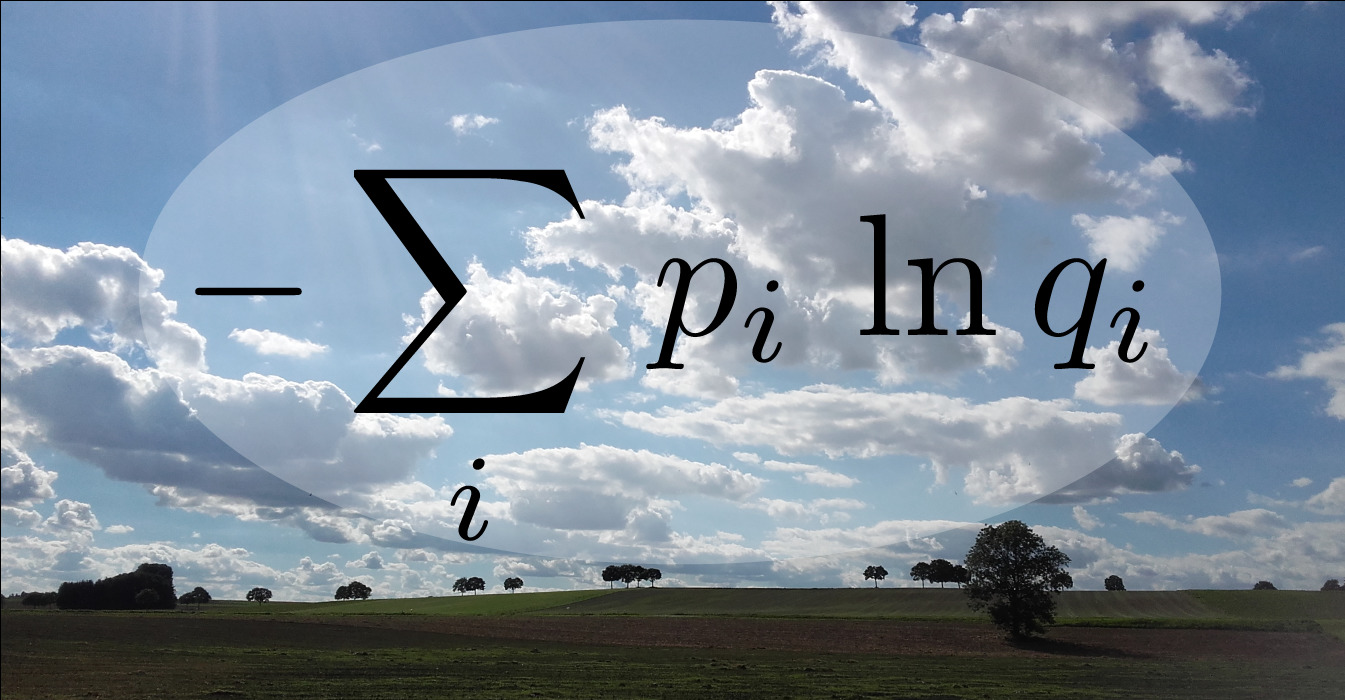
Complex predictions such as election forecasts or the weather reports often have to be simplified before communication. But how should one best simplify these predictions without facing embarrassment? In astronomical data analysis, researchers are also confronted with the problem of simplifying probabilities. Two researchers at the Max Planck Institute for Astrophysics now show that there is only one mathematically correct way to measure how embarrassing a simplified prediction can be. According to this, the recipient of a prediction should be deprived of the smallest possible amount of information.

• Learn more