| MPA-HOMEPAGE |
|
 |
"Mariage des
Maillages": Combining Spectral Methods and Finite Difference Methods in General Relativistic Hydrodynamics |
||
|
|
 Go to:
|
H. Dimmelmeier J. Novak ( J.A. Font ( J.M. Ibáñez ( E. Müller 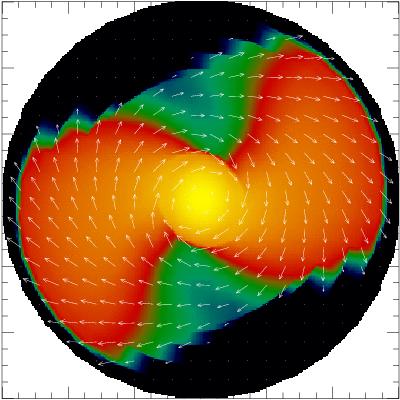 Introduction:
Introduction:
Numerical relativity is concerned with solving the Einstein equations, which are the field equations of general relativistic gravity, using computer simulations. In the 3+1 split of spacetime introduced by Arnowitt, Deser, and Misner (ADM) in 1960, the Einstein equations can be written in the form of the standard ADM metric equations. They consist of several coupled nonlinear partial differential equations, which divide into two classes: a set of time evolution equations, and a set of elliptic equations. In a dynamic situation, the evolution equations drive forward the time evolution of the spacetime.
The most common approach to numerically solve such equations is to use finite differences methods. These are particularly efficient in terms of computational speed for evolution equations. Therefore, many previous and current computer codes in numerical relativity solve only the evolution equations of the ADM metric system (free evolution method). However, a crucial tradeoff of this method is that after some evolution time the constraint equations, which are satisfied initially, are violated. These constraint violations can lead to very inaccurate results and will eventually lead to a crash of the computer code.
In the last years there have been many attempts find mathematically
equivalent reformulations of the ADM metric equations which exhibit
more robust numerical properties. Among these reformulations is the
ADM-BSSN method (originally proposed by Nakamura, Oohara, and Kojima, and
later refined by Baumgarte, Shapiro, and Shibata), which results in
numerical evolutions which are stable for a longer time compared to
the standard ADM free evolution method.
An example for a 3D general relativistic hydrodynamics code in numerical
relativity which utilizes the ADM-BSSN method is the
A completely different approach is to solve the constraint equations during the entire time evolution, which by definition prohibits constraint violations (constrained evolution). In that case however, the elliptic constraint equations have to be solved very often (i.e., at each time step). This is a severe obstacle in practical computations, as the numerical solution of elliptic equations is very time consuming even with fast modern supercomputers, if conventional finite difference methods are used.
But recently scientist have developed various alternative strategies for solving such equations efficiently. One such strategy is to use instead of finite difference methods a new class of methods, known as (pseudo-)spectral methods, where functions are not approximated by local low-order polynomials on a finite difference grid, but by global smooth functions in the form of a (small) number of coefficients. This approach is comparable to the Fourier expansion methods widely used in electrodynamics, and yields very accurate results if the desired solution is smooth (which is the case for the Einstein field equations). Spectral methods thus make it possible to use constrained evolution schemes in numerical relativity.
A very versatile and modern computational approach to using
multi-domain spectral methods in numerical relativity is provided by
the
However, one particular disadvantage of spectral methods is that they cannot accurately represent solutions which involve discontinuities such as shock fronts, which often occur in fluid dynamics. Particularly in the general multidimensional scenario of supernova core collapse, where a hydrodynamic shock drives the supernova explosion, spectral methods meet their limits. On the other hand, robust finite difference schemes to solve the fluid equations written in a hyperbolic form are known for a long time and have been employed successfully in computational fluid dynamics. In particular, the so-called high-resolution shock-capturing (HRSC) schemes have shown their advantages over other type of methods even when dealing with relativistic flows containing discontinuities. They both guarantee convergence to the physical solution of the investigated system, resolve discontinuities in the solution sharply and stably, and attain a high order of accuracy in smooth parts of the solution. Thus in the case of fluid equations, finite difference HRSC schemes are superior.
Therefore, in general relativistic numerical hydrodynamics, where
both elliptic metric equations (with smooth solutions) and hyperbolic
fluid equations (with possibly discontinous solutions) have to be
solved simultaneously, it seems a promising strategy to use spectral
methods for the former and HRSC schemes for the latter. In a computer
code following this ansatz, this involves the usage of two different
numerical grids (a spectral grid and a finite difference grid).
Following early theoretical work on this at the
Based on previous computational studies of such a combination of the
two methods in a work on spherically symmetric 1D core collapse in
tensor-scalar gravity by
[Novak and Ibáñez, 2000],
or group was the first to successfully introduce the "Mariage des
Maillage" concept in a 3D general relativistic hydrodynamics code
[Dimmelmeier, et al., 2005].
To reduce the complexity of the fully general relativistic field equations
for the spacetime metric, this code assumes conformal flatness for
the three-metric (also known as conformal flatness condition (CFC) or
Isenberg-Wilson-Mathews approximation
[Wilson, et al., 1996]), as in our
Two recent approaches to approximate or rewrite the Einstein field
equations as a system which prefers ellipticity of the equations by
[Cerda, et al., 2005] (see also our
previous work on
This work is dedicated to the memory of Jean-Alain Marck (1955-2000),
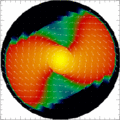
who was one of the fathers and main contributors of the In the following, we summarize some code tests and preliminary simulations, which demonstrate both the applicability of the "Mariage des Maillage" concept in a 3D general relativistic hydrodynamic code in general as well as the practical usability of that code for numerical simulations on current computer architectures. For more details, we refer to [Dimmelmeier, et al., 2005]. To ensure that the communication through the interface between the finite difference grid and the spectral grid works properly in both directions, we have performed a number of calculations which test the interpolation accuracy and efficiency. The two critical issues, on the one hand the accuracy and reduction of numerical noise in the interpolation from the finite difference grid to the spectral grid, and on the other hand the computational efficiency in the evaluation of a function represented on the spectral grid onto the finite difference grid, could be successfully resolved. We could also confirm the theoretical convergence orders of the spectral solver and the interpolation scheme in numerical calculations. Next we have made a thorough comparison of the new spectral metric solver with the two old metric solvers, which are based on a finite difference grid, in the axisymmetric case. We could numerically reproduce the expected convergence properties. Additionally, we have tested the radial fall-off behavior of the metric components, where the compactified grid of the spectral solver yields superior results. Furthermore, in a test simulation of a dynamic core collapse of a stellar core to a neutron star, we have scrutinized the proper construction of radial domains of the spectral grid. At last we have compared the results from this core collapse simulation to results of the same model evolved using a fully general relativistic hydrodynamics code without the assumption of CFC [Shibata and Sekiguchi, 2003]. The excellent agreement between these two numerical approaches further proves the applicability of the "Mariage des Maillage" concept and also shows the very good quality of the CFC approximation in the context of supernova core collapse. With the successful passing of the above tests, the code can be considered to be ready for applications which involve generic nonaxisymmetric configurations. We have first computed a nonaxisymmetric 3D test spacetime. Next we have checked the numerical stability of the code against perturbation when handling spherically or rotationally symmetric spacetimes in 3D. Finally, as the most stringent and demanding test application of a strongly relativistic 3D matter distribution, we have evolved a rapidly rotating neutron star in equilibrium, to which a strong bar-like density perturbation is added. As noticeable in the figures below, which encode the density distribution in the equatorial plane, the matter from the initial bar perturbation is partially accreted onto the neutron star, while some of it is shed and evolves into spiral arms. With the completion of this test suite we have demonstrated that in the framework of the "Mariage des Maillage" approach, spectral method can be successful implemented in a finite difference HRSC hydrodynamic code in 3D. (JavaScript must be enabled to display these figures.) The dynamics of the uniformly rotating neutron star model with a strong bar perturbation can be viewed in a movie. Color coded is the density on an equatorial slice, overplotted by vectors encoding the velocity field. The bar perturbation with a strength of 10% is initially corotating with the neutron star. As it is not in equilibrium, the central part of it is accreted onto the neutron star, while matter from the outer parts is shed into spiral arms. Note that some matter leaves the computational grid during the evolution, as the outer grid boundary is located close to the spiral arms. However, a special treatment of the boundary conditions prevents that numerical artifacts arise from this.
A more detailed overview about the "Mariage des Maillage" project, the test calculations, and the background of the envisaged applications in astrophysical simulations can be found in a color slide presentation:
|