Go to:

-Introduction
-Simulations
-References

Relativistic Hydrodynamics
Gravitational Waveform Catalog

Departamento de Astronomía y Astrofísica

Universidad de Valencia

Section of Astrophysics, Astronomy & Mechanics

Aristotle University of Thessaloniki

Departamento de Astronomía y Astrofísica

Universidad de Valencia

Neutron stars have intense or (in the case of magnetars) even extremely strong magnetic fields, which they must have acquired at some point during their lifetime. The seed for their magnetic field was laid already at their time of birth, when they formed as a proto-neutron star from a gravitationally collapsing stellar core in a supernova event. Later, as the proto-neutron star cools down and shrinks to the final neutron star, and evolves as a cold rotating neutron star, the field also undergoes an evolution and can possibly change both in strength and topology.

The dynamic emergence of a neutron star's magnetic field from the initial field configuration in the pre-collapse stellar core, and the impact on gravitational wave emission from core collapse or neutron star pulsations is an active and important field of research. If the magnetic field is sufficiently strong, it can influence the collapse dynamics itself, it can alter the neutron star's shape, and it can also shift the frequencies of pulsations that may be excited in the (proto-) neutron star by various mechanisms.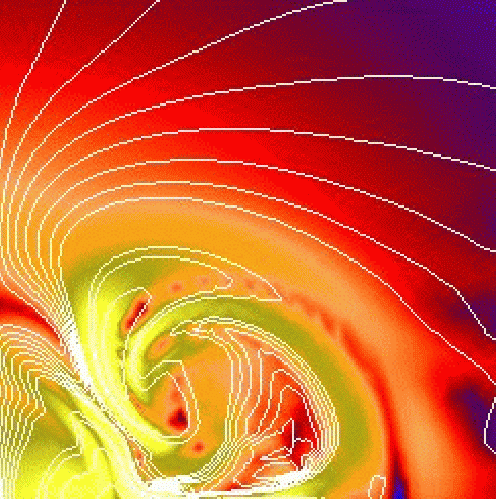

Fully dynamic simulations of the effects of magnetic field on the birth of a proto-neutron star in a supernova collapse have become feasible only very recently. Starting with a Newtonian code in [Obergaulinger, et al., 2006a] we have simulated several of our previous simple supernova core collapse models [Dimmelmeier, et al., 2002], this time with the inclusion of magnetic field of various initial strengths. This has been the most exhaustive parameter study of magneto-rotational stellar core collapse to that date. Shortly later, we have repeated this study [Obergaulinger, et al., 2006b] with a relativistic effective potential approach that approximates general relativistic effects in an otherwise Newtonian framework (as described in [Marek, et al., 2005] and later extended to rapidly rotating configurations in [Müller, et al., 2008]).

Our studies show that during the very dynamics collapse phase, when the stellar core (which weighs more than one solar mass) contracts in radius from about 1000 to 10 km and increases its central density by more than four orders of magnitude, magnetic fields can only impact the collapse noticeably if they were already extremely strong in the initial pre-collapse core, which is astrophysically very unlikely. For weak initial fields (which is the astrophysically best motivated case) there are no differences compared to purely hydrodynamic simulations without magnetic fields, neither in the collapse dynamics nor in the resulting gravitational wave signal.

In addition to that Newtonian study, which was based on a simple description of matter, recently we have presented the first general relativistic simulations of rotational supernova core collapse with models using a microphysical equation of state and including magnetic fields [Cerdá-Durán, et al., 2007] (repeating some of the models calculated without magnetic fields in [Ott, et al., 2007; Dimmelmeier, et al., 2007]), however still in the passive field approximation (where the magentic field evolves according to the fluid motion, but does not couple back to the hydrodynamics).

As expected, the results again indicate that for astrophysically motivated field strengths the magnetic field will not affect the gravitational wave emission in the collapse and early post-bounce phase, while it may become important at later post-bounce times due to various dynamo mechanisms and the prospective magneto-rotational instability. Such simulations are the first step to explaining in detail how and at what stage magnetars obtain their extremely strong magnetic fields.

• Cerdá-Durán, P., Font, J.A., and Dimmelmeier, H.,
  "General relativistic simulations of magneto-rotational core collapse with microphysics",
  Astron. Astrophys., 474, 169-191, (2007),
  [Article in astro-ph].


• Dimmelmeier, H., Font, J.A., and Müller, E.,
  "Relativistic simulations of rotational core collapse. II. Collapse dynamics and gravitational radiation",
  Astron. Astrophys., 393, 523-542, (2002),
  [Article in astro-ph].


• Dimmelmeier, H., Ott, C.D., Janka, H.-T., Marek, A., and Müller, E.,
  "Generic gravitational-wave signals from the collapse of rotating stellar cores",
  Phys. Rev. Lett., 98, 251101, (2007),
  [Article in astro-ph].


• Marek, A., Dimmelmeier, H., Janka, H.-T., Müller, E., and Buras, R.,
  "Exploring the relativistic regime with Newtonian hydrodynamics: An improved effective gravitational potential for supernova simulatio ns",
  Astron. Astrophys., 445, 273-289, (2005),
  [Article in astro-ph].


• Müller, B., Dimmelmeier, H., and Müller, E.,
  "Exploring the relativistic regime with Newtonian hydrodynamics: II. An effective gravitational potential for rapid rotation",
  Astron. Astrophys., 489, 301-314, (2008),
  [Article in astro-ph].


• Obergaulinger, M., Aloy, M.A., Dimmelmeier, H., and Müller, E.,
  "Axisymmetric simulations of magnetorotational core collapse: Approximate inclusion of general relativistic effects",
  Astron. Astrophys., 457, 209-222, (2006b),
  [Article in astro-ph].


• Obergaulinger, M., Aloy, M.A., and Müller, E.,
  "Axisymmetric simulations of magnetorotational core collapse: Approximate inclusion of general relativistic effects",
  Astron. Astrophys., 450, 1107-1134, (2006a),
  [Article in astro-ph].


• Ott, C.D., Dimmelmeier, H., Marek, A., Janka, H.-T., Hawke, I., Zink, B., and Schnetter, E.,
  "3D collapse of rotating stellar iron cores in general relativity including deleptonization and a nuclear equation of state",
  Phys. Rev. Lett., 98, 261101, (2007),
  [Article in astro-ph].