Go to:

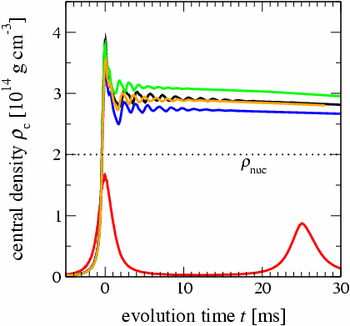-Introduction
-Simulations
-Summary Table
-References

Relativistic Hydrodynamics
Gravitational Waveform Catalog

General relativity plays a major role in the collapse and explosion of massive stars because of the extreme compactness of the remnant neutron star. An accurate modelling of the supernova explosion mechanism must also include a realistic treatment of the microphysics, such as sophisticated neutrino transport and a realistic equation of state, which has as yet been combined with full relativity in one-dimensional simulations only.

Since numerical stability issues, exceedingly high computational costs, and the sheer complexity of the equations pose a serious obstacle for realistic multi-dimensional supernova simulations in general relativity, we have pursued a different approach, namely that of approximating the effects of relativity by using a stronger "effective gravitational potential" instead of the usual Newtonian one, while remaining strictly within the framework of Newtonian dynamics. With the help of this modified potential, any Newtonian hydrodynamics code for stellar core collapse (with elaborate microphysics included) can be extended into the moderately relativistic regime with negligible effort.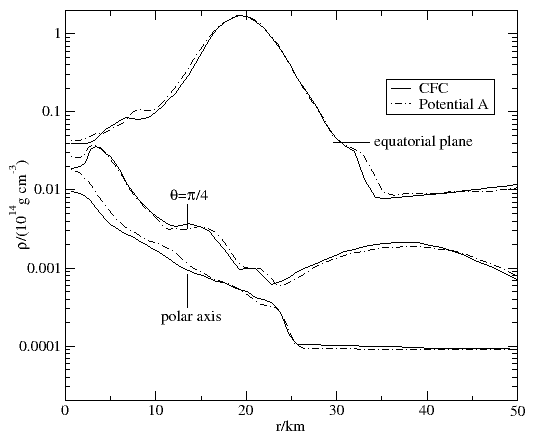

Simulations:

For spherical configurations, it is possible to construct an effective potential (the "TOV potential") from a comparison of the relativistic Tolman-Oppenheimer-Volkoff (TOV) equations with the Newtonian equations of hydrostatic equilibrium [Rampp & Janka, 2002]. This potential gives the correct density stratification for spherical neutron stars in equilibrium, and also works quite well for dynamical phenomena such as core collapse. A comparison of realistic supernova simulations using a progenitor model from Woosley and Weaver [Woosley & Weaver, 1995] revealed only minor discrepancies between the TOV potential as used in the Vertex radiative transport code and the fully relativistic treatment of the Agile-BoltzTran code [Liebendörfer et al., 2005]. Those observed discrepancies are due to the coupling of the relativistic TOV potential with Newtonian hydrodynamics, which leads to a spurious increase of the gravitational mass during collapse. Subsequent studies have shown that slight modifications of the TOV potential can solve this problem, leading to almost perfect agreement with the relativistic reference [Marek et al., 2005].

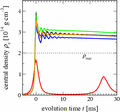
The figure on the left, for example, shows the evolution of shock position for the TOV potential and modified potentials A and B, and with the relativistic Agile-BoltzTran code. The potentials A and B perform significantly better than the TOV potential, for which the shock recedes too quickly from 50 ms after bounce onward. Bearing in mind that the jump of the shock between 170 ms and 200 ms is due to a different handling of shock discontinuities in both codes and not to the modelling of gravity, the agreement with the fully relativistic treatment is very good.

If the pseudo-Newtonian treatment is extended to multi-dimensional simulations, with the spherical effective potential replacing the spherical part of the Newtonian one, the agreement with general relativity was found to deteriorate for rapid differential rotation. Recently, we have incorporated additional relativistic corrections for strong rotation into potential A (the best effective potential in spherical symmetry), and now observe very good agreement for a substantial range in the degree of rotation.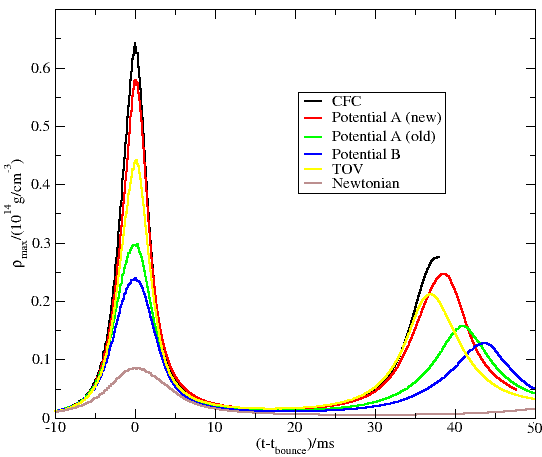

The quality of the new potential has been tested in purely hydrodynamic simulations with a simplified analytic equation of state for the axisymmetric models studied by Dimmelmeier, Font, and Müller [Dimmelmeier, et al., 2001, Dimmelmeier, et al., 2002a, Dimmelmeier, et al., 2002b] in the CFC approximation to general relativity [Wilson, et al., 1996]. The improvement can be clearly seen in the figure above, which shows the evolution of the maximum density during collapse for the centrifugal bounce model A2B4G1.

Here the spherical effective potentials (TOV, A (old) and B) underestimate the maximum density at bounce by 30% or more, while the new potential A comes within 10% of the CFC result. In the figure below, we also show the excellent agreement between the new potential and CFC for the density stratification of the extremely fast rotating model A4B5G5 at bounce. Furthermore, we have been able to extract gravitational wave signals with a mean error of less than 10% compared to CFC.

Summary Table:

A comparison of the maximum densities during bounce and after ring-down for the old and new effective potential A and for the CFC approximation can be found in a PDF table.

References:

• Dimmelmeier, H., Font, J.A., and Müller, E.,
  "Gravitational waves from relativistic rotational core collapse",
  Astrophys. J. Lett., 560, L163-L166, (2001),
  [Article in astro-ph].


• Dimmelmeier, H., Font, J.A., and Müller, E.,
  "Relativistic simulations of rotational core collapse. I. Methods, initial models, and code tests",
  Astron. Astrophys., 388, 917-935, (2002),
  [Article in astro-ph].


• Dimmelmeier, H., Font, J.A., and Müller, E.,
  "Relativistic simulations of rotational core collapse. II. Collapse dynamics and gravitational radiation",
  Astron. Astrophys., 393, 523-542, (2002),
  [Article in astro-ph].


• Liebendörfer, M., Rampp, M., Janka, H.-T., and Mezzacappa, A.,
  "Supernova simulations with Boltzmann neutrino transport: A comparison of methods",
  Astrophys. J., 620, 840-860, (2005),
  [Article in astro-ph].


• Marek, A., Dimmelmeier, H., Janka, H.-T., Müller, E., and Buras, R.,
  "Exploring the relativistic regime with Newtonian hydrodynamics: An improved effective gravitational potential for supernova simulations",
  Astron. Astrophys., in print, (2005),
  [Article in astro-ph].


• Rampp, M. and Janka, H.-T.,
  "Radiation hydrodynamics with neutrinos. Variable Eddington factor method for core-collapse supernovae simulations",
  Astron. Astrophys., 396, 361-392, (2002),
  [Article in astro-ph].


• Wilson, J.R., Mathews, G.J., and Marronetti, P.,
  "Relativistic numerical model for close neutron-star binaries",
  Phys. Rev. D, 54, 1317-1331, (1996),
  [Article in gr-qc].


• Woosley, S.E. and Weaver, T.A.,
  "The evolution and explosion of massive stars. II. Explosive hydrodynamics and nucleosynthesis",
  Astrophys. J. Suppl., 101, 181-235, (1995),
  [Article in PDF format via ADS].