MPA HOMEPAGE 
contact press site map disclaimer deutsch
Zurueck zur Startseite
 

  Current Research Highlight :: January 2011 all highlights

Data analysis and steam engines

As astronomical telescopes become more and more sensitive, the analysis techniques become ever more sophisticated. But do we need a new theoretical approach for a modern image reconstruction method? Not necessarily, a well-known theory, originally developed for a better understanding of steam engines, does the trick: thermodynamics. Two researchers at the Max Planck Institute for Astrophysics have now shown that the so called Gibbs energy in thermodynamics, known for more than a century, can be applied to the development of new, optimal imaging techniques.

Fig. 1: The development of powerful steam engines during the industrial revolution benefited from the theory of thermodynamics.
Copyright: linkPfeilExtern.gifBy Lardner, Dionysius and by F.A. Brockhaus, Berlin und Wien [both Public domain], via Wikimedia Commons

Fig. 2: Sky image of the galactic magnetic field as seen by the Faraday rotation effect on radio emissions (top) and a map of the statistical error of this image (bottom). The image was reconstructed from some 38,000 individual measurements using a mathematical method based on the concept of Gibbs energy.
Original Data: NVSS catalog and Taylor et al. (2010).
Image reconstruction: Oppermann et al. (2010)

Thermodynamics describes the molecular chaos that you find for instance inside a steam engine. It is impossible to calculate the positions and velocities of the each of the countless molecules in a boiler. However, if an engineer is interested in the typical velocities of these molecules, to determine the pressure in the boiler for example, he can use thermodynamics. This theory provides us with reliable calculations of such global properties by simplifying the very complicated dynamics of the individual molecules through statistical arguments.

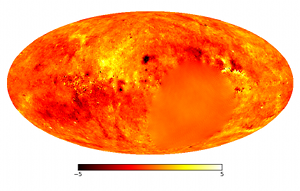
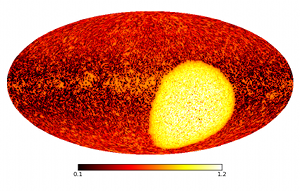
Modern astronomers collect light from outer space to produce astronomical images in different wavelengths. At a first glance there is not much common ground with the typical applications of thermodynamics. When dealing with observations, however, there are also uncertainties that can only be dealt with in a statistical sense. The sky brightness has to be determined for theoretically an infinite number of pixels; but the data are coarse-grained, washed-out, noisy, most often incomplete, and always finite. Intelligent methods are needed to convert the telescope data into the most accurate image of the sky.

Unfortunately there are often an infinite number of possible images of the sky to match the observational data. These possibilities are just as confusing as the molecular chaos in a boiler but can be dealt with using the same statistical methods. In a steam engine, the behaviour of the water molecules is governed by two parameters: the internal energy U of the water and its entropy S. The former is the mean energy of the molecules due to their motion and the intramolecular attractive forces. The latter describes the amount of molecular chaos: the larger the entropy the more violent the motion. Thermodynamics postulates that the water will reach an equilibrium, so that the combination of internal energy, entropy and temperature T is minimised. This combination is called Gibbs energy: G = U - TS, and helps to understand water at different temperatures. At low temperatures the water molecules want to minimise their internal energy and therefore form drops or crystals. At high temperatures, they will form a gas, which even though energetically costly is very chaotic (and therefore has large entropy).

Torsten Enßlin and Cornelius Weig from the Max Planck Institute for Astrophysics have now shown that the same terms, internal energy, entropy and Gibbs energy, can be applied to the problem of reconstructing digital images. The entropy describes the uncertainty of assigning a particular brightness to the individual sky pixels. The internal energy describes the probability of the various sky images, which have to be taken into account within the boundaries given by the uncertainty. The best possible sky image can then be calculated from the interplay between internal energy and entropy. Moreover, in contrast to traditional techniques, the new method also gives an error map, showing the uncertainty of all pixels.

The researchers were able to show that many long established imaging algorithms are based on this approach, which originated in the century-old thermodynamics. However, completely new algorithms can be developed as well. The entropy concept was already known in image reconstruction theory, but the internal energy, which is needed to determine the Gibbs energy, had not been introduced as such. The same thermodynamical laws contributing to the industrial revolution could again play an important role in today’s development of information technologies.


Torsten Enßlin and Cornelius Weig


References:

Torsten A. Enßlin and Cornelius Weig, "Inference with minimal Gibbs free energy in information field theory", Phys. Rev. E 82, 051112 (2010)
linkPfeilExtern.gifhttp://pre.aps.org/abstract/PRE/v82/i5/e051112 linkPfeilExtern.gifhttp://arxiv.org/abs/1004.2868

Niels Oppermann, Henrik Junklewitz, Georg Robbers, Torsten A. Enßlin, "Probing Magnetic Helicity in Different Astrophysical Contexts", submitted, arXiv:1008.1246
linkPfeilExtern.gifhttp://arxiv.org/abs/1008.1246

Taylor, A. R.; Stil, J. M.; Sunstrum, C., "A Rotation Measure Image of the Sky", Volume 702, Issue 2, pp. 1230-1236 (2009)
linkPfeilExtern.gifhttp://iopscience.iop.org/0004-637X/702/2/1230/

Links

linkPfeil.gifResearch Highlight August 2009


drucken.gif print version topPfeil.gif Top
© 2003—2022, Max-Planck-Gesellschaft, München
last modified: 2010-12-22