 |
|
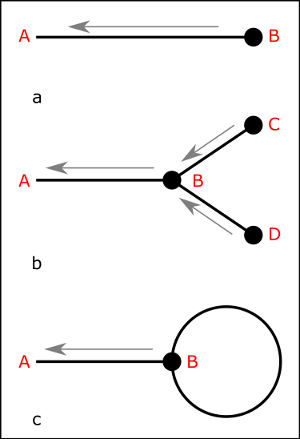
Abb. 1:
Die Feynman-Diagramme bestehen aus Punkten und
Linien. Punkte am Ende von Linien bezeichnen so genannte
Informationsquellen, also die Information die die Messdaten über
einen Punkt im Raum enthalten (siehe Diagramm (a)). In Linien
eingebettete Punkte bezeichnen dagegen Datenverarbeitungsschritte die
verschiedene Informationen kombinieren (siehe Diagramm (b)). Die
Linien beschreiben Informationspropagation: Was sagt mir eine
Informationsquelle am Ort B über mein Signal am Orte A aus? Jedes
der möglichen Diagramme beschreibt eine Rechenvorschrift, einen
Algorithmus, der auf die Daten angewendet werden muss. Die Summe der
Ergebnisse der einzelnen Diagramme liefert dann die gewünschte
Antwort, beispielsweise das mittlere Signal gegeben Daten und
Vorwissen.
|
 |
 |
|
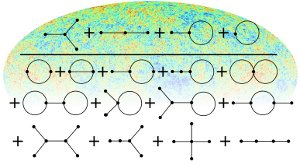
Abb. 2:
Diagramme zur Bestimmung der durch die Inflation
verursachten Abweichung der CMB Temperaturfluktuationen von einer
Normalstatistik. Die Temperaturwerte des CMB-Himmels (hier
farbkodiert) müssen die gezeigten Diagramme durchlaufen. In die
Endpunkte der Diagramme müssen die Temperaturwerte jeden
Himmelspunktes eingehen, die dann gemäß der vom Diagramm
vorgegebenen Rechenvorschrift verarbeitet werden. Die angegebene
Kombinationen der Diagramme liefern dann ein Maß der
statistischen Abweichung und somit eine Messung einer wichtigen
Signatur der Inflation. Der Zähler dieser Formel, bestehend aus
vier Diagrammen, ist bereits in nicht-diagrammatischer Form in der
Fachliteratur bekannt. Der Nenner jedoch, der auch die
Messunsicherheit der Methode kodiert, ist nur in einer wesentlich
gröberen Form zuvor bekannt gewesen.
|
|  |
Die menschlichen Sinne wie Hören, Sehen und Fühlen erlauben
es unserem Gehirn, ein detailliertes Modell unserer Umgebung zu
kreieren, obwohl die menschlichen Sinne keineswegs perfekt sind und
unser Gesichtsfeld oft eingeschränkt ist. Dieses Kunststück
vollbringt unser Gehirn durch das Hinzuziehen von Erfahrungswerten
über die Beschaffenheit unserer Umwelt.
Auch künstliche Sinne, seien es Kameras, Mikrophone oder
astronomische Teleskope, sind keineswegs perfekt und erfordern daher
komplexe Interpretationen und Benutzung von Zusatzwissen. Kosmologen
beispielsweise möchten die Verteilung der Materie im Universum
genau vermessen, haben aber das Problem, dass 85 Prozent der Materie
unsichtbar sind. Vom Rest sind allenfalls sporadisch Galaxien
sichtbar, die nur zu oft den Teleskopen entgehen. Daher bieten die
Galaxiendaten nur ein unvollständiges und verrauschtes Abbild der
kosmischen Materieverteilung. Die Materieverteilung stellt in diesem
Fall das Signal dar, welches aus den Daten herausgelesen werden soll.
Da es eine Unzahl möglicher Materieverteilungen gibt, stellt sich
die Frage, welche davon das richtige Signal ist. Leider hätten
unendlich viele verschiedene Signale exakt die gleichen Daten erzeugen
können. Allerdings sind nicht alle Möglichkeiten gleich
plausibel. So ist es beispielsweise wenig wahrscheinlich, dass die
kosmische Materieverteilung in dem durch unsere Galaxie verdeckten
Bereich vollkommen anders aussieht als im übrigem Bereich, nur
weil wir diesen zufälligerweise nicht gut beobachten
können. Auch von einem nur teilweise sichtbaren Menschen
würden wir kaum annehmen, dass er drei Beine hat, nur weil wir
diese gerade nicht sehen können. Exotischen Signalkonfigurationen
kann also von vornherein eine geringe Wahrscheinlichkeit zugeordnet
werden.
Damit können Fragen gestellt werden wie: Welches Signal ist
gemessen an Daten und Vorwissen am plausibelsten? Wie groß ist
die Unsicherheit dieser Schätzung des Signals?
Die Forscher am Max-Planck-Institut für Astrophysik konnten
zeigen, dass solche Fragestellungen sich als statistische Feldtheorie,
genauer gesagt als Informationsfeldtheorie, formulieren lassen. Diese
ist zwar sehr komplex, aber dank der Teilchenphysik existieren
mächtige mathematische Werkzeuge zu ihrer Berechnung. So kann man
ihnen beispielsweise mit so genannten Feynman-Diagrammen approximative
Lösungen abringen (siehe Abbildung 1). Die Diagramme sind dabei
graphische Darstellungen der Datenverabeitungsschritte.
Nicht alle der resultierenden Algorithmen sind vollkommen neu. So
entspricht das einfachste der Diagramme (Abbildung 1a) dem seit 60
Jahren erfolgreich eingesetzten Wiener Filter. Komplexere Diagramme
(Abbildung 1b&c) lassen sich aus den einzelnen Rechenschritten des
Wiener Filters aufbauen und erlauben auch Signalerkennungsprobleme zu
lösen, die mit dem Wiener-Filter alleine nicht optimal
behandelbar wären. Die Informationsfeldtheorie liefert hier
maßgeschneiderte Algorithmen für die jeweiligen
Signalerkennungsprobleme.
Erste Anwendungen dieser neuen Methodik werden in der Kosmologie
liegen. So wurden bereits optimale Methoden zur kosmischen
Kartographie mittels Galaxienvermessungen entwickelt, die die
bisherigen linearen Analysemethoden verbessern sollten (siehe
 Aktuelle Forschung, Oktober 2008). Aktuelle Forschung, Oktober 2008).
Auch über das frühe Universum kurz nach dem Urknall lassen
sich mittels Informationsfeldtheorie genauere Erkenntnisse
gewinnen. Das früheste Abbild des Universums wird uns durch die
Reststrahlung des Urknalls, den kosmischen Mikrowellenhintergrund
(engl. cosmic microwave background, CMB) vermittelt. Dieser gibt ein
Abbild des heißen Gases, dass das Universum 380.000 Jahre nach
dem Urknall erfüllt hat und enthält Informationen aus den
allerersten Sekundenbruchteilen unseres Universum, als während
einer so genannten Inflationsepoche der Raum praktisch explodierte.
Der CMB kann von Satelliten wie dem kürzlich gestarteten Planck
Surveyor
( Planck-Nachrichten),
aufgenommen werden. Aber Planck wird auch viele Störsignale
auffangen, die eine direkte Interpretation seiner Daten kompliziert
macht. Zum Beispiel blockt Strahlung unserer eigenen Galaxie einen
Teil des CMB-Himmels ab und die Sensoren des Satelliten erzeugen ein
ungewolltes Rauschen in den Daten. Um trotz dieser Störsignale
die subtilen Signaturen der Inflation aus den Temperaturschwankungen
detektieren zu können, wurden mittels der Informationsfeldtheorie
verbesserte Analysemethoden entwickelt (Abbildung 2). Planck-Nachrichten),
aufgenommen werden. Aber Planck wird auch viele Störsignale
auffangen, die eine direkte Interpretation seiner Daten kompliziert
macht. Zum Beispiel blockt Strahlung unserer eigenen Galaxie einen
Teil des CMB-Himmels ab und die Sensoren des Satelliten erzeugen ein
ungewolltes Rauschen in den Daten. Um trotz dieser Störsignale
die subtilen Signaturen der Inflation aus den Temperaturschwankungen
detektieren zu können, wurden mittels der Informationsfeldtheorie
verbesserte Analysemethoden entwickelt (Abbildung 2).
Die Anwendung der Informationsfeldtheorie ist keineswegs auf die
Kosmologie beschränkt. Bildgebende Verfahren in Medizin, Geologie
und Materialwissenschaften können möglicherweise von der
Theorie profitieren. Sollte es soweit kommen, würde ein weiteres
Beispiel für einen unerwarteten Spin-off von Grundlagenforschung
geschaffen: Methoden der mathematischen Physik, die zur Berechnung von
sehr abstrakten teilchenphysikalischen Vorgängen entwickelt
wurden, fänden in Form von Software Einzug in Arztpraxen und
Ingenieurbüros.
Torsten Enßlin, Mona Frommert
Publication
Torsten A. Enßlin, Mona Frommert, Francisco S. Kitaura,
"Information field theory for cosmological perturbation reconstruction
and non-linear signal analysis",
2008, submitted
 arXiv:0806.3474 arXiv:0806.3474
|

