At the beginning of the universe, just after its birth but before the Big Bang when the universe became hot, our cosmos expanded exponentially during a very short period called cosmic inflation. This process is an indispensable building-block of the standard model of the universe; however, we do not yet know which physical mechanism caused this inflation.

The standard inflation scenario is described by a nearly de Sitter space-time. In this framework, there are ten isometric transformations, i.e. mappings that preserve distances: three spatial translations; three spatial rotations; one time translation accompanied by spatial dilation; and three additional isometries, which reduce to special conformal transformations as time approaches infinity.

As the expansion rate is necessarily time-dependent (because inflation must end) this breaks the time translation symmetry and hence the spatial dilation symmetry, limiting how much the universe deviates from dilation invariance. In terms of observations, such dilation invariance would give precisely scale-invariant initial fluctuations for the early universe, whereas a small deviation has been detected from CMB data by Planck with more than 5 sigma significance.

In the usual model of inflation, six of the ten isometries remain unbroken: translations and rotations. But why must they remain unbroken while the others are broken? In fact, slight deviations from rotation symmetry naturally arise in "anisotropic inflation" models, in which a scalar field is coupled to a vector field. A violation of rotational symmetry also occurs when very long-wavelength perturbations on super-horizon scales are coupled with short-wavelength perturbation. Finally, a pre-inflationary universe was probably very chaotic and highly anisotropic, and thus a remnant of the pre-inflationary anisotropy may still be detectable. These models lead to a quadrupolar modulation of the primordial two-point correlation function, whose fractional strength is parametrized by g_*. When g_* is different from zero, the strength of the two-point correlation function depends on the angle between the line connecting the two points and some preferred direction in space.

We tested the rotational symmetry by searching for such a preferred direction using the two-point correlation function of primordial perturbations. More precisely, we studied the CMB anisotropy, which is linearly related to the primordial perturbations. For our analysis, we used the CMB temperature data from the Planck mission released in 2013, which is publicly available at the Planck Legacy Archive. As the main "CMB channel" we use the map at 143 GHz, because at this frequency the contamination from synchrotron, free-free and dust emission of our own galaxy is weaker than in other, higher frequency channels. To further reduce the diffuse Galactic emission we fitted templates to the 143 GHz map and subsequently removed them from the observed maps. These foreground templates are created by subtracting one frequency map from the map at an adjacent frequency - similar to the "SEVEM"-method of the Planck collaboration.

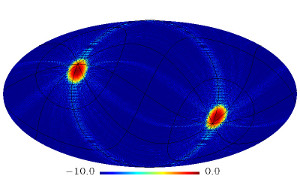
From this preliminary analysis, we detect a significant quadrupolar modulation of the CMB power spectrum (g_* = -0.116 +/- 0.014 at 68% confidence level) with a direction close to the Ecliptic pole. This is shown in Figure 1a.

However, there is another effect which causes asymmetry. The Planck beams at 143 GHz are not circular; the orientation of their semi-major axes is parallel to Planck's scan direction, which lies approximately along the Ecliptic longitudes. This means that the beams are "fatter" along the Ecliptic longitudes, and thus the Planck satellite measures less power along the Ecliptic north-south direction than in the east-west direction. In the data, this yields a quadrupolar power modulation (with g_* < 0).

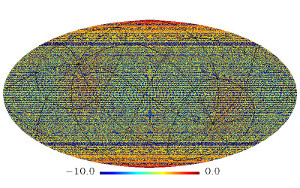
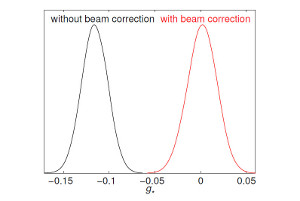
After quantifying and removing the effect of this beam asymmetry, the rotation asymmetry in the CMB basically vanishes (g_* = 0.002 +/- 0.016 at 68% confidence level). In Figure 1b, we show the probable locations of a preferred direction estimated with a correction for the beam asymmetry and Figure 2 shows the likelihood of the fractional strength of the quadrupole modulation, which peaks at zero, when the correction is added.

In a final step we tested the effect of the Galactic foreground emission on our estimate. When we use the raw 143 GHz map without foreground cleaning, we find significant anisotropy both before and after the beam asymmetry correction (g_* = 0.305 and 0.295 +/- 0.015, respectively). The direction in this case lies close to the Galactic pole; the foreground reduction thus plays an important role in nulling artificial anisotropy in the data.

In a nutshell: After removing the effects of Planck's asymmetric beams and of the Galactic foreground emission, we find no evidence for any rotational asymmetry in our early Universe, which would be predicted by anisotropic inflation models. Our limit (less than 2%) provides the most stringent test of rotational symmetry during inflation so far.

Jaiseung Kim and Eiichiro Komatsu