 |
 |
|
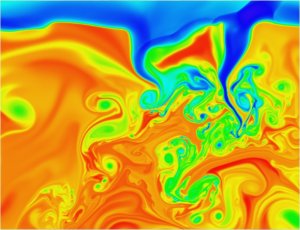
Abb. 1:
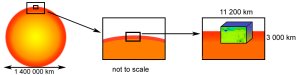
Die Abbildung zeigt ein 2600 km breites und 2000 km
tiefes Gebiet. Horizontale und vertikale Auflösung betragen jeweils 3 km
bzw. 2 km. Die Region befindet sich in einem 11200 km breiten und 3000 km
tiefen Gebiet, das mit einer Auflösung von 12 km mal 8 km simuliert wird.
Das obere Bild zeigt die Simulation, das untere die Grössenverhältnisse.
Die dargestellte Größe ist die Entropie. Sie hängt eng mit der Temperatur
zusammen und erlaubt es, den Ursprung des Gases leichter zu verfolgen. Gas
mit hoher Entropie ist rot dargestellt und stammt weiter aus dem Inneren.
Gas mit niedriger Entropie ist blau dargestellt und wurde in den
Oberflächenschichten abgekühlt. Zwischenwerte werden grün und gelb
dargestellt. Diese treten auch am Übergang zwischen den sichtbaren
Schichten (oben) zu den unterhalb verborgenen Schichten auf, als scharfe,
aber glatte Grenze im obersten Teil der Abbildung.
|
 |
 |
|
Abb. 2:
Der Film zeigt die Entwicklung der Temperatur
im selben Gebiet für dieselbe Simulation wie in Abb. 1, aber zu
einem früheren Zeitpunkt. Er illustriert die Entwicklung von
einem Zustand, wie er auch in niedriger Auflösung beobachtet
werden kann (erstes Bild) bis zur Ausbildung kleinskaliger Strukturen
(bereits nach den ersten 40 von 262 Einzelbildern). Die gezeigte
Größe ist die Differenz zwischen der lokalen Temperatur und
der horizontal gemittelten Temperatur (beide auf einer logarithmischen
Skala). Überdurchschnittlich heiße Gebiete sind rot
dargestellt, überdurchschnittlich kalte blau, Gebiete mit
Durchschnittstemperaturen grün. Dünne schwarze Linien
verbinden Orte mit identischer Differenz zwischen dem Druck und seinem
horizontalen Mittel. Diese Darstellung ähnelt daher einer
Wettervorhersagekarte. Zu beachten ist hier, daß die senkrechte
Richtung (X) tatsächlich der Vertikalen in der Simulation
entspricht (Y bezeichnet die horizontale Richtung, angedeutet durch
die Pfeile) und in einer Wettervorhersagekarte die Isolinien Orte mit
gleichem lokalen Druck verbinden. (Langversion des
 Films, 32 MB) Films, 32 MB)
|
 |
 |
|
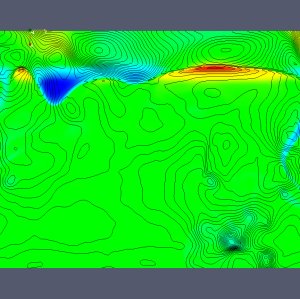
Abb. 3:
Der Film zeigt ein Gebiet, das in jeder
horizontalen Richtung (Y, Z) 4000 km breit ist und 2000 km tief
(X). Horizontale und vertikale Auflösung betragen jeweils 10 km
bzw. 7 km. Diese Region ist in ein 11200 km breites und 3000 km tiefes
Gebiet eingebettet, das mit einer horizontalen Auflösung von 40
km und einer vertikalen von 28 km simuliert wird. Die dunkelgelbe
Oberfläche verbindet alle Punkte mit einer Temperatur von 8000
K. Eine spezielle räumliche Darstellung (volume rendering) wird
benutzt, um große Druckunterschiede sichtbar zu machen. Die
dafür ausgesuchte physikalische Größe ist die Norm
(Länge) des Gradienten der Differenz zwischen lokalem Druck und
dessen horizontalem Mittel (beide in logarithmischen Einheiten). Orte
mit großen lokalen Druckschwankungen erscheinen
rot. Mäßig große Druckschwankungen sind blau
dargestellt, Zwischenwerte in grün und hellgelb.
|
|  |
Beobachtungen unserer Sonne zeigen ein bekanntes Granulationsmuster
von hellen Strukturen im sichtbaren Licht (den Granulen), die in ein
Netzwerk aus Gas mit viel geringerer Helligkeit eingebettet sind. Im
Durchschnitt dehnen sich solche Granulen etwa 1200 km weit
aus. Innerhalb der Granulen ist das Gas heißer als in seiner
Umgebung und bewegt sich aufwärts mit etwa 2 km/s bis die
Abstrahlung in den Weltraum zu ausreichender Abkühlung
führt. Nachdem es seitwärts aus der Granule verdrängt
wurde, sinkt das kalte und dichte Gas abwärts als Teil eines
Netzwerks, das die Granulen umgibt. Die besten Instrumente, die
derzeit für Aufnahmen der Sonnenoberfläche verfügbar
sind, können Details mit einer Größe von 70 km
erkennen (Beispiele:
 NAOJ, NAOJ,
 Institute for Solar Physics).
Bei dieser Auflösung erscheinen
die Granulen bemerkenswert glatt. Numerische Simulationen der
Sonnengranulation ergaben bei ähnlicher Auflösung genau das
gleiche Resultat. Was würden wir finden, wenn wir dieselben
Schichten in der Sonne ansehen könnten, aber Details mit einer
Größe von nur wenigen km erkennen könnten? Da jede
Granule auch durch ihre Umgebung beeinflußt wird, müssen
numerische Simulationen dieses Vorgangs für ein wesentlich
größeres Gebiet durchgeführt werden, das mehr als
10000 km breit und 3000 km tief sein sollte. Selbst auf massiv
parallelen Computern muß dabei eine kleinere Region
ausgewählt werden, für die das zeitabhängige Verhalten
solch kleiner Strukturen untersucht werden soll. Dieses Teilgebiet
enthält bloß einige wenige Granulen. Seine Umgebung wird
mit einer geringeren Auflösung numerisch simuliert. Abb. 1 zeigt
eine solche Simulation, bei der aber nur eine horizontale Richtung
berücksichtigt wurde. Die Sonnenoberfläche ist klar
sichtbar als Gebiet von geringer vertikaler Ausdehnung, das im
horizontalen Verlauf aber stark gekrümmt erscheint und dadurch
unterschiedlich tief liegt. Die meisten kleinen Strukturen sind in den
wenigen Fronten zu finden, die sich innerhalb der sichtbaren
Sonnenatmosphäre nach oben bewegen. Dieses Bild stimmt mit
Aufnahmen von der Sonnenoberfläche und in der physikalischen
Literatur beschriebenen Vorstellungen gut überein, aber hier
betrachten wir dasselbe Phänomen mit viel höherer
Auflösung. Das Gebiet unterhalb der Oberfläche sieht
allerdings völlig anders aus: Je länger das Gas Zeit gehabt
hat, ins Innere abzusinken, um so mehr kleine Details werden
sichtbar. Die kleinräumigen Strukturen werden hauptsächlich
von den Scherkräften zwischen den Auf- und Abströmgebieten
erzeugt. Institute for Solar Physics).
Bei dieser Auflösung erscheinen
die Granulen bemerkenswert glatt. Numerische Simulationen der
Sonnengranulation ergaben bei ähnlicher Auflösung genau das
gleiche Resultat. Was würden wir finden, wenn wir dieselben
Schichten in der Sonne ansehen könnten, aber Details mit einer
Größe von nur wenigen km erkennen könnten? Da jede
Granule auch durch ihre Umgebung beeinflußt wird, müssen
numerische Simulationen dieses Vorgangs für ein wesentlich
größeres Gebiet durchgeführt werden, das mehr als
10000 km breit und 3000 km tief sein sollte. Selbst auf massiv
parallelen Computern muß dabei eine kleinere Region
ausgewählt werden, für die das zeitabhängige Verhalten
solch kleiner Strukturen untersucht werden soll. Dieses Teilgebiet
enthält bloß einige wenige Granulen. Seine Umgebung wird
mit einer geringeren Auflösung numerisch simuliert. Abb. 1 zeigt
eine solche Simulation, bei der aber nur eine horizontale Richtung
berücksichtigt wurde. Die Sonnenoberfläche ist klar
sichtbar als Gebiet von geringer vertikaler Ausdehnung, das im
horizontalen Verlauf aber stark gekrümmt erscheint und dadurch
unterschiedlich tief liegt. Die meisten kleinen Strukturen sind in den
wenigen Fronten zu finden, die sich innerhalb der sichtbaren
Sonnenatmosphäre nach oben bewegen. Dieses Bild stimmt mit
Aufnahmen von der Sonnenoberfläche und in der physikalischen
Literatur beschriebenen Vorstellungen gut überein, aber hier
betrachten wir dasselbe Phänomen mit viel höherer
Auflösung. Das Gebiet unterhalb der Oberfläche sieht
allerdings völlig anders aus: Je länger das Gas Zeit gehabt
hat, ins Innere abzusinken, um so mehr kleine Details werden
sichtbar. Die kleinräumigen Strukturen werden hauptsächlich
von den Scherkräften zwischen den Auf- und Abströmgebieten
erzeugt.
Solch kleine Strukturen treten nicht auf, sofern nicht ein
Mindestmaß an räumlicher Auflösung erreicht wird und
fortgeschrittene numerische Rechenverfahren in den Simulationen
verwendet werden. Dieser Gesichtspunkt wurde durch Simulationen mit
niedrigerer Auflösung sowie mit anderen numerischen Verfahren
überprüft. Die eben beschriebenen Resultate werden dabei
durch das Ergebnis unterstützt, daß verschiedene Verfahren
immer ähnlicher werdende Resultate liefern, sobald ein bestimmte
räumliche Auflösung überschritten wird. Da die
hochgradig turbulenten Strukturen in der Strömung in Abb. 1 von
Schichten von undurchsichtigem Gas verdeckt werden (der sichtbaren
Sonnenoberfläche), müssen indirekte Beobachtungsverfahren
herangezogen werden. Eine Möglichkeit sind Oszillationen und
Wellen, die von der Strömung erzeugt werden. Die Sonne pulsiert
bekanntermaßen und diese Pulsationen sind die beste "Sonde", die
zur Untersuchung des Sonneninneren verfügbar ist. Es handelt sich
dabei um (stehende) Schallwellen, die in der Sonnenhülle
bleiben. Die meiste Energie wird in den Schichten unmittelbar
unterhalb der Sonnenoberfläche in diese Wellen übertragen,
gerade da, wo auch die kleinskaligen Strukturen in Abb. 1
erscheinen. Eine Analyse dieser Simulationen zeigt zahlreiche
"akustische Ereignisse", Pulse, die in den Grenzgebieten von Auf- und
Abströmungen entstehen, wo große Scherkräfte auftreten
und Gebiete niedriger Dichte plötzlich komprimiert werden
können. Abb. 2 zeigt einen Film, der diese Pulse als schwarze
Linien darstellt. Sie verbinden Orte, an denen der gleiche Unterschied
zwischen lokalem und horizontal gemitteltem Druck herrscht. Diese
Druckschwankungen bewegen sich meist in einer Richtung, die nicht mit
der lokalen Strömung zusammenhängt. Letztere wird hier durch
die Zeitentwicklung der Temperaturschwankungen sichtbar
(farbcodiert). Die Pulse kreuzen einander, werden gedämpft oder
verstärkt und manche schaffen es bis an die Oberfläche. In
welchem Zusammenhang stehen sie zu den beobachteten Oszillationen?
Denn diese finden eigentlich auf den Längenskalen einiger
Granulen und noch größer statt.
Um diese Frage zu beantworten sind noch realistischere Simulationen
nötig, die beide horizontalen Raumrichtungen
berücksichtigen. Die Einschränkung auf zwei räumliche
Dimensionen erzeugt Phänomene, die für die reale Konvektion
in der Sonne nicht erwartet (und auch nicht beobachtet) werden, wie
etwa die stabilen Wirbel sowohl in Abb. 1 als auch im Film in Abb. 2
(diese gelangen jedoch nicht bis zur Oberfläche). Die
Rechenanforderungen für solch dreidimensionale Simulationen sind
beträchtlich und dieselbe Auflösung wie in Abb. 2 zu
erreichen bedeutet, die heutigen, leistungsfähigsten
Supercomputer bis an die Grenzen ihrer Möglichkeiten zu
bringen. Abb. 3 zeigt Resultate aus einer ersten Reihe solcher
Simulationen, bei etwa einem Drittel der Auflösung, wie sie im
zweidimensionalen Fall erzielt wurde. Der Anstieg an Komplexität
in der Strömung ist klar erkennbar, wenn die Entwicklung vom
Anfangsstadium (bei einer Auflösung, die effektiv mit jener
vergleichbar ist, die in Bildern von der Sonnenoberfläche mit den
leistungsfähigsten Instrumenten erreicht wird) bis zu ihrem
Abschlußstadium verfolgt wird. In realer Zeit auf der Sonne ist
das nur ein paar Minuten später, etwas kürzer als die
Entwicklung, die in Abb. 2 gezeigt wird. Die glatte Oberfläche
bezeichnet eine Temperaturregion gerade unterhalb der sichtbaren
Schichten der Sonne und ihre Entwicklung zeigt, wie die
Aufströmgebiete mit der Zeit zerfallen (und neu entstehen) und
wie ihre Grenzen zu den Abströmgebieten durch Scherkräfte
zerrissen werden. Mit der Zeit tauchen Fronten mit starken
Druckunterschieden auf (gelb-rot), besonders entlang der Grenzen der
Aufströmgebiete (dem Innen liegenden Teil der Granulen), die sich
weiter nach oben bewegen. Das Auftreten dieser Phänomene und der
drastische Anstieg an Komplexität innerhalb starker
Abströmgebiete ist der Anlaß zu Simulationen mit einer
ähnlichen Auflösung wie in Abb. 2, um die Rolle der
Scherkräfte bei der Entstehung von Schallwellen in der Sonne zu
klären. Diese werden nun als teil eines bewilligten Projektes im
Rahmen von
 DEISA
durchgeführt. Jedoch ist bereits jetzt klar
erkennbar, daß das, was von außen bei der bisher
erreichten Auflösung in den Beobachtungen glatt aussieht, recht
verschieden erscheint, wenn weiterentwickelte Methoden verwendet
werden, mit denen wir auch unter die Sonnenoberfläche mit hoher
Auflösung schauen können. DEISA
durchgeführt. Jedoch ist bereits jetzt klar
erkennbar, daß das, was von außen bei der bisher
erreichten Auflösung in den Beobachtungen glatt aussieht, recht
verschieden erscheint, wenn weiterentwickelte Methoden verwendet
werden, mit denen wir auch unter die Sonnenoberfläche mit hoher
Auflösung schauen können.
Friedrich Kupka, Herbert J. Muthsam, Christof Obertscheider, Florian Zaussinger
Reference:
Muthsam et al., Mon. Not. Roy. Astr. Soc. 380, 1335-1340 (2007)
doi:10.1111/j.1365-2966.2007.12185.x
|





