|

Go to:
-Model A3B2G4
-Model A3B2G5
-Model A1B3G5
-Model A2B4G1
-Model A4B5G5
 Axisymmetric Core Collapse Axisymmetric Core Collapse
 Relativistic Hydrodynamics Relativistic Hydrodynamics
 Waveform Catalog Waveform Catalog
|
 |
H. Dimmelmeier
J.A. Font ( Departamento de Astronomía y Astrofísica, Departamento de Astronomía y Astrofísica,
 Universidad de Valencia, Spain) Universidad de Valencia, Spain)
E. Müller
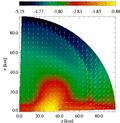
Movies of four representative core collapse models:
These movies show the collapse dynamics together with the evolution of
the maximum density and the gravitational wave signal of four
representative core collapse models in relativstic gravity.
In the left box, the logarithm of the density in a quadrant of the
core is color coded. The density is scaled to nuclear matter density,
i.e. nuclear matter density corresponts to 0. On top of this, velocity
vectors of the meridional velocity
vr + vtheta
are shown, scaled to the maximum per frame. Note that the vertical
axis corresponds to the rotation axis, and that the radial scale
changes during the movie.
In the upper right box, the evolution of the gravitational wave
amplitude
AE220
is plotted, and the lower right box shows the evolution of the maximum
density rhomax. Note that for
non-toroidal models, the maximum density is identical to the central
density.
 |

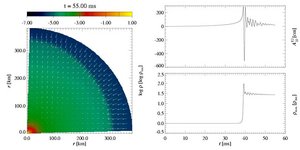
- Model A3B2G4:
This is a regular collapse model. Its initial model has moderate
differential rotation and a low rotation rate
betarot ini = 0.5%.
With a subnuclear adiabatic index
gamma1 = 1.30, the core
collapses moderately fast within roughly 40 ms, and subsequently
forms a stable remnant. This is clearly visible in the evolution of
the maximum density. After the bounce, ringdown oscillations can be
identified in this plot.
The gravitational wave signal is typical for a Type I waveform,
with a pronounced negative peak immediately after core bounce, and
subsequent ringdown oscillations.
The rotation plays only a minor role in the collapse dynamics. Both
the density distribution, the meridional velocity vectors, and the
shock front exhibit only small deviations from spherical symmetry.
After the formation of the shock front, its outward propagation can be
followed in the left box.
 Movie in MPG format (8 MB). Movie in MPG format (8 MB).
 Movie in AVI format (5 MB). Movie in AVI format (5 MB).

 |

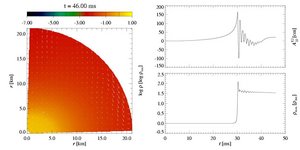
- Model A3B2G5:
This is a rapid collapse model. Its initial model has moderate
differential rotation and a low rotation rate
betarot ini = 0.5%.
With a low subnuclear adiabatic index
gamma1 = 1.28, the core
collapses rapidly within roughly 30 ms, and subsequently
forms a stable remnant. This is clearly visible in the evolution of
the maximum density. After the bounce, the ringdown oscillations are
strongly suppressed.
The gravitational wave signal is typical for a Type III waveform,
with no strong negative peak immediately after core bounce, and
only small amplitude ringdown oscillations. Due to the missing
large negative peak, the maximum signal amplitude of such models is
comparably small.
The rotation plays only a minor role in the collapse dynamics. Both
the density distribution, the meridional velocity vectors, and the
shock front exhibit only small deviations from spherical symmetry.
After the formation of the shock front, its outward propagation can be
followed in the left box. Later, an inward zoom shows the stable
core remnant, which is particularly dense in this type of collapse.
 Movie in MPG format (11 MB). Movie in MPG format (11 MB).
 Movie in AVI format (9 MB). Movie in AVI format (9 MB).

 |

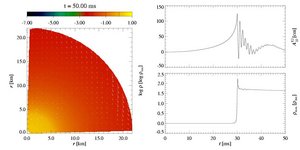
- Model A1B3G5:
This is a rapid collapse model. Its initial model has almost uniform
rotation and a moderate rotation rate
betarot ini = 0.9%.
With a low subnuclear adiabatic index
gamma1 = 1.28, the core
collapses rapidly within roughly 30 ms, and subsequently
forms a stable remnant. This is clearly visible in the evolution of
the maximum density. After the bounce, the ringdown oscillations are
strongly suppressed.
The gravitational wave signal is typical for a Type III waveform,
with no strong negative peak immediately after core bounce, and
only small amplitude ringdown oscillations. Due to the missing
large negative peak, the maximum signal amplitude of such models is
comparably small.
The rotation plays only a minor role in the collapse dynamics. Both
the density distribution, the meridional velocity vectors, and the
shock front exhibit only small deviations from spherical symmetry.
After the formation of the shock front, its outward propagation can be
followed in the left box. Later, an inward zoom shows the stable
core remnant, which is particularly dense in this type of collapse.
 Movie in MPG format (9 MB). Movie in MPG format (9 MB).
 Movie in AVI format (7 MB). Movie in AVI format (7 MB).

 |

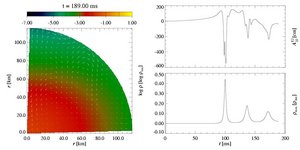
- Model A2B4G1:
This is a multiple bounce collapse model. Its initial model has
moderate differential rotation and a medium rotation rate
betarot ini = 1.8%.
With a subnuclear adiabatic index
gamma1 = 1.325 close to the
initial value gammaini = 4 / 3, the core
collapses slowly within roughly 100 ms, and subsequently
undergoes several phases of re-expansion and contraction. This is
clearly visible in the evolution of the maximum density. Eventually, a
stable remnant will form, but on a timescale much longer than the
collapse time.
The gravitational wave signal is typical for a Type II waveform,
with distinct strong negative peaks synchronous with each of the
separate bounces.
In this collapse type, rotation plays a crucial role in the collapse
dynamics. Due to angular momentum conservation, the core collapse is
stopped at subnuclear densities by the strong centrifugal
forces.
In each subsequent bounce, the zoom in the left box follows the
outward re-expansion and the following contraction to the next
bounce. The formation of a new shock front after each bounce is
clearly visible.
 Movie in MPG format (8 MB). Movie in MPG format (8 MB).
 Movie in AVI format (5 MB). Movie in AVI format (5 MB).

 |

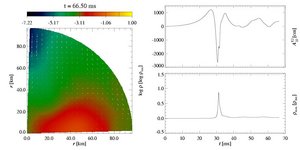
- Model A4B5G5:
This is an extremely rapidly and differentially rotating collapse
model. Its initial model has strong differential rotation and a high
rotation rate betarot ini = 4.0%.
As a consequence, the initial density distribution is already toroidal.
To overcome the additional stabilization by the strong rotation, the
model has a small subnuclear adiabatic index
gamma1 = 1.28. The core
collapses rapidly within roughly 30 ms, and spins up
considerably, displaying an increasingly pronounced toroidal density
distribution. It bounces at supernuclear densities, but then
re-expands again to form a stable remnant at a much lower subnuclear
density. This is clearly visible in the evolution of the maximum
density.
The gravitational wave signal exhibits a single peak, which can be
attributed to the core bounce. As such extremely rapidly and
differentially rotating cores have a toroidal shape and thus a large
quadrupole moment, their maximum signal amplitudes are exceptionally
high.
In this collapse type, rotation has a strong influence on the collapse
dynamics. While at the pole the contraction proceeds almost unaffected by
centrifugal forces, it is slowed down considerably along the
equator. After bounce, a strongly anisotropic shock front and large
scale velocity vortices are created, leading to the formation of a
short-lived accretion disk. The anisotropy of the shock front is
amplified by the toroidal density distribution of the pre-shock
matter.
After core bounce, a strong jtabetlike outflow can be observed along the
rotation axis, while the region around the stable torus is still
surrounded by the velocity vortices which have formed in the
post-shock region after the bounce.
After the formation of the shock front, its outward propagation can be
followed in the left box. Later, an inward zoom shows the stable
toroidal core remnant, which exhibits and off-centered and not very
dense maximum in this type of collapse.
 Movie in MPG format (10 MB). Movie in MPG format (10 MB).
 Movie in AVI format (8 MB). Movie in AVI format (8 MB).

 |
 Comments to: Harald Dimmelmeier Comments to: Harald Dimmelmeier  harrydee@mpa-garching.mpg.de harrydee@mpa-garching.mpg.de
|  |