|
| MPA-HOMEPAGE | |
|
|
|
 |
 |
Molecular Physics | |
|
MPA Homepage > Scientific Research > Research Groups
> Molecular Physics |
|
 |
Go to:
|
|
Focus
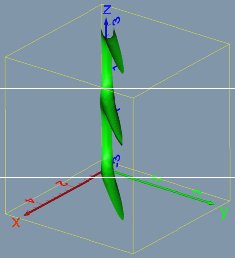Empirically derived Hund's rules of the pre-quantum-mechanics era predict the ordering of the energy levels possessing different spin and orbital angular momentum quantum numbers. They have proved to be almost universally valid for atoms, molecules, and quantum dots. Yet, despite of a long standing debate the search for their origin persists, primarily due to the lack of the precise knowledge of the electronic structure in different spin states. We explore the origin of the first Hund rule for a two-dimensional model of He-like systems and that of two-electron quantum dots. These models represent ideal systems providing a direct fundamental insight into the structure of the internal part of the fully-correlated wave functions, allowing an unambiguous argument. An examination of their probability density distributions reveals indeed the existence of a region in the internal space where the singlet wave function has a smaller probability density than the corresponding triplet one. Due to the presence of this conjugate Fermi hole the singlet probability density has to migrate far away from the center of the one-electron potential. This rationalizes the well-known broader electron density distribution of the singlet state relative to the corresponding triplet. This key observation explains the singlet-triplet energy gap.
Origin of the first Hund rule and the structure of Fermi holes
in two-dimensional He-like atoms and two-electron quantum dots. (Manuscript)
|
|
