Nucleosynthesis and Instabilities in Core Collapse Supernovae

deutsch

On February 23rd, 1987, astronomers became witnesses of a gigantic supernova explosion in the Large Magellanic Cloud. This supernova, named SN 1987 A, terminated the life of Sk -69 202, a blue supergiant star, about 15-20 times more massive than our Sun.

SN 1987 A was the nearest supernova observed since 383 years and provided us with a wealth of unprecedented, high-quality observational data during the following days and months, against which astrophysicists could test their theoretical models of supernova explosions developed during the last three decades. In these models a shock wave forms during the collapse of the stellar core to a neutron star, triggers explosive thermonuclear burning and eventually expels the entire stellar envelope.

However, it was soon learned from SN 1987A that the hitherto available models, which were computed in one spatial dimension, (i.e. under the assumption of spherical symmetry) could not fully account for a number of observations. Already in August 1987 gamma-ray (and associated X-ray) emission from the radioactive decay of Co56 to Fe56 was detected. This isotope is originally synthesized as Ni56 in the inner silicon and oxygen-rich layers of the star next to the collapsed core. Its early detection proved that large-scale mixing processes took place during the explosion and transported this material near to the stellar surface. This was a big surprise and forced theorists to carry out simulations of the explosion in more than one spatial dimension. But only now, twelve years after SN 1987A, have computers and numerical methods become fast enough that it is possible to follow (nearly) the complete evolution within the first hours of the explosion with sufficient resolution.

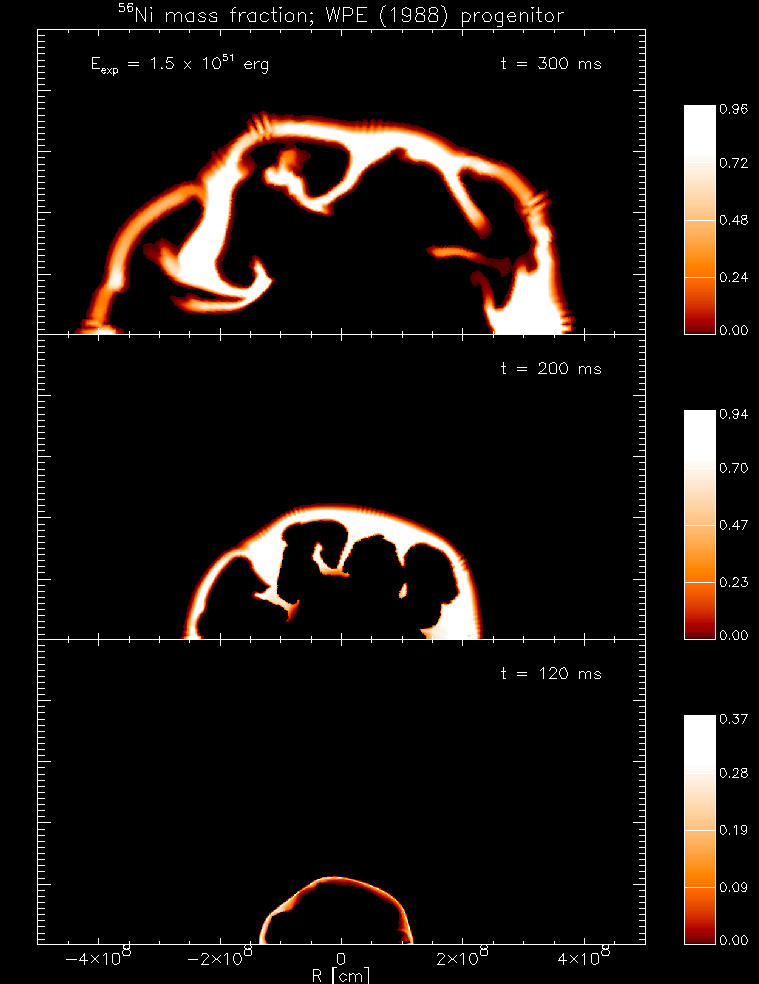
Figure 1

Figure 1 shows how the Ni56 is synthesized in one of our 2D simulations during the first 0.3 s of the explosion in the innermost 10000 km of the star. The shock wave (coinciding with the outermost boundary of the shell visible for t=120 ms and 200 ms) is heated by neutrinos from a newly born neutron star in the center and overruns the material in the silicon shell, thereby heating it to more than 5 billion degrees and burning it to Ni56. Different from one-dimensional models the Ni56 (bright regions) is not confined to a spherical shell. Its distribution shows several filaments and "blobs" which are distorted by convective instabilities in the neutrino-heated regions.

Figure 2

Hydrodynamic instabilities of the Rayleigh-Taylor type are of crucial importance during the later phases of the evolution as shown in Figure 2, which depicts the density distribution 300 s after the launch of the shock wave. The shock is visible as the outermost blue discontinuity at a radius of about 3 million km. It has left behind a dense shell (visible as a red ring) at the boundary between the stellar hydrogen envelope and the helium core. The Rayleigh-Taylor instability has led to the formation of clumps which contain the Ni56 and other newly synthesized elements and has mixed this material through a significant fraction of the stellar helium core with velocities of up to 4000 km/s.

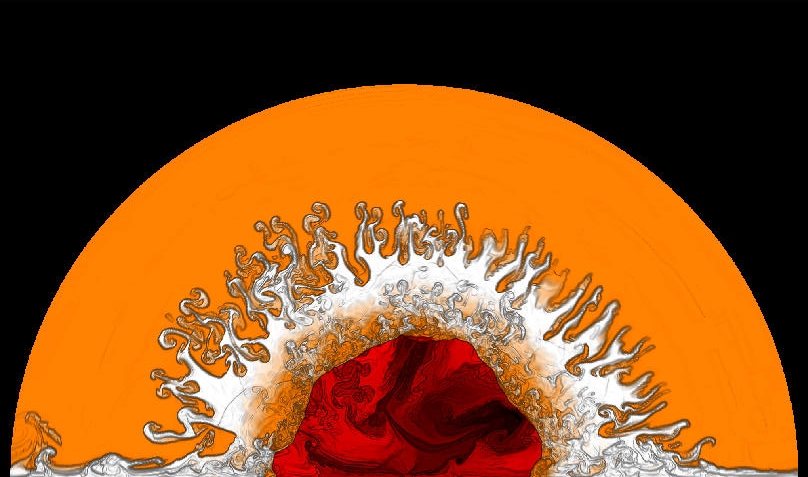
Figure 3

10,000 s after its birth the shock has already left the stellar surface. Figure 3 shows the density distribution at this time in a region with a diameter of 65 million km, approximately corresponding to the original size of the star. The nickel-rich clumps have penetrated into the dense shell and have been substantially decelerated and mixed into their surroundings. The outer boundary of the dense shell shows pronounced Rayleigh-Taylor mixing of low-density, hydrogen-rich (orange) and dense helium-rich material (white). However, the current two-dimensional models do not yield the mixing of Ni56 (and its decay products) into the (outer) hydrogen envelope seen in SN 1987A. This might hint towards a globally asymmetric explosion of this supernova.

K. Kifonidis, T. Plewa, H.-Th. Janka, E. Müller





Further information:

• The First Five Minutes of a Core Collapse Supernova: Multidimensional Hydrodynamic Models, K. Kifonidis, T. Plewa, H.-Th. Janka, E. Müller, Preprint astro-ph 9911407
• Nucleosynthesis and Clump Formation in a Core Collapse Supernova, K. Kifonidis, T. Plewa, H.-Th. Janka, E. Müller, Preprint astro-ph 9911183