 |
|
Abb. 1:
Bild des Gravitationslinsensystems B1608 + 656, aufgenommen mit dem Hubble
Space Telescope (von Suyu et al. 2010). Die zentrale Linsengalaxie (G1) und
eine Satellitengalaxie (G2) sind durch mehrere Bilder der Hintergrundquelle (A,
B, C und D) umgeben. Die Reihenfolge der Bilder folgt der Ankunftszeit des
Lichtsignals.
(c) HST/NASA
|
 |
 |
|
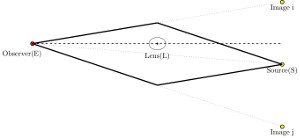
Abb. 2:
Konfiguration eines starken Gravitationslinsensystems. Die durchgezogene Linie
zeigt zwei unterschiedliche Wege, der von der Quelle emittierte Photonen folgen
können. Die gestrichelten Linien deuten die Winkelpositionen an, unter denen
die Bilder und die Quelle am Himmel erscheinen würden. Die Position der Quelle
kann jedoch üblicherweise nicht beobachtet werden, da sie sehr nahe an der Linse
ist. Man beachte, dass dieses Schema nicht maßstabsgetreu ist: Die Entfernung,
die die Photonen zurücklegen, ist viel größer als die Ausdehnung der Linse oder
der Quelle.
Credit: Jee, Komatsu and Suyu 2014
|
 |
 |
|
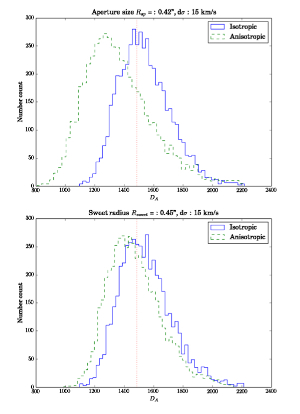
Abb. 3:
Verteilung der gemessenen Winkeldurchmesser-Entfernungen von simulierten Daten
für die über die Apertur gemittelte und mit der Leuchtkraft gewichtete
projizierte Geschwindigkeitsdispersion für das Linsensystem B1608 + 656 (siehe
Abbildung 1). Die blaue durchgezogene Linie zeigt die Verteilung, wenn das
Eingangsmodell isotrop ist, die grüne gestrichelte Linie für eine anisotrope
simulierte Geschwindigkeitsdispersion. Die Entfernung kann mit einer Genauigkeit
von etwa 15% bestimmt werden. Wenn man das radiale Profil der
Geschwindigkeitsverteilung berücksichtigt (mit dem "Sweet Spot", siehe Text),
verringert sich die Unsicherheit auf nur 12%.
Credit: Jee, Komatsu and Suyu 2014
|
|  |
Bei der Beobachtung des Universums gibt es ein grundlegendes Problem: das
3-dimensionale Universum wird auf die 2-dimensionale Betrachtungsebene
projiziert, wodurch es schwer ist, die "Tiefe" des Universums zu bestimmen
(anders gesagt: es ist schwierig zu messen, wie weit ein Objekt von uns
entfernt ist). Infolgedessen müssen sich die Astronomen auf indirekte Methoden
verlassen, um kosmologische Entfernungen zu messen.
Hierfür gibt es zwei Methoden: Bei dem Verfahren der sogenannten
"Standardkerzen" nimmt man an, dass die absolute Helligkeit eines Objekts
bekannt ist. Diese wird dann mit der scheinbaren Helligkeit verglichen. So
führte beispielsweise dieses Verfahren mit Typ-Ia Supernovae als Standardkerzen
zur Entdeckung der beschleunigten Expansion des Universums und der Existenz der
Dunklen Energie. Die andere Methode nutzt einen „Standardmaßstab“, der die
scheinbare Größe eines Objekts mit seiner intrinsischen Größe vergleicht. Zum
Beispiel konnten die Astronomen große Galaxiendurchmusterungen verwenden, um
die so genannten „baryonischen akustischen Schwingungen“ als Standardmaßstab zu
nutzen.
Allerdings haben beide bestehenden Methoden ihre Grenzen. Da wir die Vorläufer
der Typ Ia-Supernovae immer noch nicht kennen, könnte diese Art der
Entfernungsbestimmung durch unser physikalisches Verständnis der Supernovae
begrenzt sein. Für die Messung der baryonischen akustischen Schwingungen ist
ein hoher Einsatz an Ressourcen notwendig, da wir die Spektren von Millionen
von Galaxien aufnehmen müssen; ein derartiges Projekt dauert viele Jahre und
zig Millionen Euro. Deshalb besteht gibt es einen starken Wunsch nach anderen
Standardkerzen oder Standardmaßstäben, die physikalisch gut verstanden sind und
weniger Beobachtungsressourcen benötigen.
Wissenschaftler am MPA haben vor kurzem ein Verfahren wesentlich verbessert, um
Gravitationslinsensysteme mit gemessenen Zeitverzögerungen zu nutzen, um die
Entfernung zur Gravitationslinse abzuleiten. Die Methode wurde erstmals 2009
von Paraficz und Hjorth vorgeschlagen; seitdem wurden aber keine weiteren
Untersuchungen durchgeführt. Der starke Gravitationslinseneffekt tritt dann
auf, wenn sich eine massereiche Galaxie fast, aber nicht exakt, auf der
Sichtlinie zu einem Hintergrund-Quasar befindet. Das von der Quelle emittierte
Licht durchquert das Gravitationsfeld der Galaxie und wird dabei leicht in
Richtung der Galaxie gebogen; ein Effekt der Allgemeinen Relativitätstheorie.
Auf jedes Photon, das einen unterschiedlichen Bereich der Galaxie durchquert,
wirkt ein anderes Gravitationspotential. Dadurch wirkt die Galaxie wie eine
optische Linse, und die Photonen mit unterschiedlichen Wegen produzieren
mehrere Bilder rund um die Galaxie (siehe Abbildung 1). Da jedes Photons einen
anderen Weg zum Beobachter nimmt, unterscheiden sich die Pfadlängen und damit
die Ankunftszeiten der Photonen. Der Betrachter kann dann die zeitliche
Verzögerung zwischen den verschiedenen Wegen messen, wenn die Quelle ihre
Helligkeit mit der Zeit ändert (siehe Schema in Abbildung 2 ). Der
Zeitunterschied zwischen den Bildern wird als Zeitverzögerung bezeichnet.
Die Physik hinter dieser neuen Methode ist einfach. Die gemessene
Zeitverzögerung ist proportional zur Masse der Galaxie. Die gemessene
Geschwindigkeitsdispersion der Galaxie verrät das Gravitationspotential der
Linse. Eine Kombination dieser beiden Messungen ergibt somit die physikalische
Größe der Linse: Vergleicht man die physikalische Größe der Linse, die
berechnet wurde, und die Winkelgröße der Linse, die beobachtet wurde, so erhält
man den Abstand zur Linse.
Die so gemessene Winkeldurchmesser-Entfernung zur Linsengalaxie kann dann mit
anderen Messgrößen wie etwa der Zeitverzögerung, der
Geschwindigkeitsdispersion, der Rotverschiebung der Gravitationslinse und den
Positionen der Mehrfachbilder in Bezug gesetzt werden. Sie hängt außerdem davon
ab, wie steil das Massenprofil der Gravitationslinse ist, das über eine Analyse
der Form und Helligkeitsverteilungen der Gravitationslinse und der
Mehrfachbilder bestimmt werden kann.
Ein großer Vorteil dieser neuen Methode, der von den Wissenschaftlern am MPA
entdeckt wurde, besteht darin, dass sich jegliche Wirkung einer äußeren Masse
aufhebt, die sich entlang der Sichtlinie zwischen dem Beobachter und der Quelle
befindet - die sogenannte "externe Konvergenz". Mit anderen Worten, die
Winkeldurchmesser-Entfernung ändert sich nicht durch die Anwesenheit einer
äußeren Masse, die eine zusätzliche Biegung der Lichtstrahlen bewirkt.
Grundsätzlich wirkt die externe Konvergenz wie eine zusätzliche Linse und trägt
zur Unsicherheit bei traditionellen Entfernungsmessungen mit starken
Gravitationslinsen bei. Eine gute Analogie besteht zur klassischen Optik: Es
ist unmöglich, zwischen einem einzelnen Linsensystem mit einer gegebenen
Brennweite und einem Mehrfachlinsensystem aus Linsen mit unterschiedlichen
Brennweiten, die zusammen ein System mit der gleichen effektiven Brennweite
bilden, zu unterscheiden. Ebenso können Gravitationslinsensysteme mit einer
einzigen Linse und mit mehrere Linsengalaxien nicht durch die Beobachtungen
unterschieden werden.
Allerdings, hängt die Winkeldurchmesser-Entfernung bei unserem Verfahren nicht
von der externen Konvergenz ab, da die Zeitverzögerung und die
Geschwindigkeitsverteilung allein durch die Eigenschaften der Linse bestimmt
sind. Wird diese Methode auf das bestehendes Linsensystem B1608 + 656
(Abbildung 1) angewandt, so kann die Entfernung mit einer Genauigkeit von 15%
gemessen werden (Abb. 3).
Dieses neue Verfahren erfordert eine genaue Abschätzung der Masse und des
Gravitationspotentials des Systems aus den beobachteten Daten. Die besonderen
Herausforderungen liegen dabei sowohl bei der Beobachtung als auch bei der
Modellierung der Gravitationslinse: Unter der Annahme, dass die Linsengalaxie
(in den meisten Fällen eine massereiche elliptische Galaxie) das dynamische
Gleichgewicht erreicht hat, wirkt die zufällige Bewegung der massereichen
Teilchen, aus denen die Galaxie besteht, der Schwerkraft entgegen, so dass die
Galaxie weder zusammenbricht noch sich ausdehnt. Dies misst man durch die
Geschwindigkeitsdispersion von Sternen in Bezug auf die Mitte der Galaxie. Die
Jeans-Gleichung liefert einen Zusammenhang zwischen der radialen Komponente der
Geschwindigkeitsdispersion und dem Gravitationspotential; es ist jedoch
unmöglich, nur die radiale Komponente der Geschwindigkeitsdispersion zu
beobachten. Die Messung beruht auf der Dopplerverschiebung des Sternenlichts.
Dies bedeutet, dass nur die Komponente der Geschwindigkeitsdispersion entlang
der Sichtlinie gemessen werden kann. Da man nur leuchtende Objekte (wie Sterne)
messen kann, ergibt sich bei der Beobachtung eine projizierte
Geschwindigkeitsdispersion, die mit der Lichtstärke gewichtet ist. Ist die
Geschwindigkeitsdispersion anisotrop, so wird die Situation sogar noch
komplizierter. Darüber hinaus wird die gemessene Geschwindigkeitsdispersion in
der Regel über einen gewissen Öffnungswinkel gemittelt, typischerweise wenigen
Zehntel Bogensekunden. Am Ende ist es also nicht ganz einfach, den
Beobachtungswert mit dem Potential in Beziehung zu setzen.
Um dieser Komplikation Herr zu werden, verwenden wir ortsaufgelöste
spektroskopische Daten der Linsengalaxie, um das radiale Profil der
Geschwindigkeitsdispersion zu erhalten. Außerdem verwenden wir einen Radius,
bei dem die Streuung zwischen verschiedenen anisotropischen Profilen minimiert
wird, den sogenannten "Sweet Spot", der am MPA bereits früher von anderen
Forschern abgeleitet wurde (Churazov et al.). Mit diesem Verfahren reduziert
sich die Unsicherheit aus der anisotropen Geschwindigkeitsdispersion und die
Bestimmung der Winkeldurchmesser-Entfernung verbessert sich auf eine
Genauigkeit von nur 12%.
Diese Studie zeigt, dass mit einem System, bei dem eine Galaxie als starke
Gravitationslinse wirkt und für das die Zeitverzögerungen gemessen wurden, die
Winkeldurchmesser-Entfernung genau bestimmt werden kann. Dies stellt eine
leistungsstarke, neue Möglichkeit zur Verfügung, unser Universum zu kartieren.
Inh Jee, Eiichiro Komatsu and Sherry H. Suyu(ASIAA)
References:
Inh Jee, Eiichiro Komatsu, Sherry H. Suyu, Measuring angular diameter
distances of strong gravitational lenses,  arXiv:1410.7770 arXiv:1410.7770
|




